
分析 (1)通过计算得出三边对应成比例,可判定其相似.
(2)∠A=∠A′,再证出$\frac{AB}{A′B′}=\frac{AC}{A′C′}$,即可得出相似.
解答 解:(1)△ABC∽△A′B′C′;理由如下:
∵$\frac{AB}{A′B′}=\frac{4}{12}$=$\frac{1}{3}$,$\frac{BC}{B′C′}=\frac{6}{18}$=$\frac{1}{3}$,$\frac{AC}{A′C′}$=$\frac{8}{24}$=$\frac{1}{3}$,
∴$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{AC}{A′C′}$,
∴△ABC∽△A′B′C′;
(2)△ABC∽△A′B′C′;理由如下:
∵$\frac{AB}{A′B′}=\frac{7}{3}$,$\frac{AC}{A′C′}=\frac{14}{6}=\frac{7}{3}$,
∴$\frac{AB}{A′B′}=\frac{AC}{A′C′}$,
又∵∠A=∠A′=120°,
∴△ABC∽△A′B′C′.
点评 本题主要考查了相似三角形的判定定理;熟练掌握相似三角形的判定定理是解决问题的关键.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
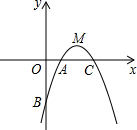 已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M.
已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | -$\frac{10}{3}$ | C. | $\frac{10}{3}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com