
分析 根据题意可以得到三种方案的价格,从而可以比较三种价格的高低.
解答 解:方案Ⅲ的价格>方案Ⅱ的价格>方案Ⅰ的价格.
理由:设这种产品的价格原价为a,根据题意可得,
方案Ⅰ为:a(1+p%)(1-p%);
方案Ⅱ为:a(1+p%)(1+q%);
方案Ⅲ为:a(1+$\frac{p+q}{2}$%)(1+$\frac{p+q}{2}$%).
∵a(1+p%)(1-p%)<a(1+p%)(1+q%),
∴方案Ⅱ的价格>方案Ⅰ的价格.
∵a(1+p%)(1+q%)=a(1+p%+q%+p%q%),
a(1+$\frac{p+q}{2}$%)(1+$\frac{p+q}{2}$%)=a(1+p%+q%+$\frac{p+q}{2}$%$\frac{p+q}{2}$%),
p,q是不相等的正数,
∴$\frac{p+q}{2}$•$\frac{p+q}{2}$=$\frac{(p+q)^{2}}{4}=\frac{{p}^{2}+{q}^{2}+2pq}{4}$$>\frac{2pq+2pq}{4}$=pq.
∴$\frac{p+q}{2}$%$\frac{p+q}{2}$%>p%q%.
∴a(1+p%+q%+$\frac{p+q}{2}$%$\frac{p+q}{2}$%)>a(1+p%+q%+p%q%).
即方案Ⅲ的价格>方案Ⅱ的价格.
由上可得,a(1+$\frac{p+q}{2}$%)(1+$\frac{p+q}{2}$%)>a(1+p%)(1+q%)>a(1+$\frac{p+q}{2}$%)(1+$\frac{p+q}{2}$%).
∴方案Ⅲ的价格>方案Ⅱ的价格>方案Ⅰ的价格.
点评 本题考查列代数式和式子的大小比较,解题的关键是能根据题意列出代数式,能将式子变形之后进行大小的比较.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
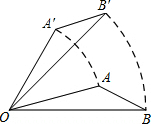 如图,将△AOB绕点O按逆时针旋转45°后得到△A′OB′,若∠AOB=15°,则∠A′OB的度数是( )
如图,将△AOB绕点O按逆时针旋转45°后得到△A′OB′,若∠AOB=15°,则∠A′OB的度数是( )| A. | 25° | B. | 30° | C. | 35 | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com