
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).
).
(1)![]() _____,点A的坐标为______,点B的坐标为_____;
_____,点A的坐标为______,点B的坐标为_____;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;

【答案】(1)-3(-1,0),(3,0)(2)9
【解析】
(1)把点C的坐标代入函数解析式,然后求出k的值即可;令y=0,得到关于x的一元二次方程,解方程求出x的值,再根据点A在点B的左边,写出坐标即可;
(2)把抛物线解析式整理成顶点式,然后写出顶点坐标,再连接OM,分别求出△AOC、△MOC、△MOB的面积,然后根据四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积进行计算即可求解;
(1)∵抛物线y=x22x+k与y轴交于点C(0,3),
∴k=3,
∴抛物线的解析式为y=x22x3,
令y=0,则x22x3=0,
∴(x+1)(x3)=0,
∴x+1=0,x3=0,
解得x1=1,x2=3,
∴点A的坐标为A(1,0),点B的坐标为B(3,0);
故答案为:3,(1,0),(3,0);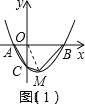
(2)如图(1),∵y=![]() 2x3=
2x3=![]() 4,
4,
∴抛物线的顶点为M(1,4),连接OM,
则△AOC的面积=![]() AOOC=
AOOC=![]() ×1×3=32,△MOC的面积=
×1×3=32,△MOC的面积=![]() OC|xM|=
OC|xM|=![]() ×3×1=
×3×1=![]() ,
,
△MOB的面积=![]() OB|yM|=
OB|yM|=![]() ×3×4=6,
×3×4=6,
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=![]() +
+![]() +6=9.
+6=9.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,AB=4,点
,AB=4,点![]() 是边
是边![]() 上动点(点
上动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() .
.

(1)求![]() 的大小;
的大小;
(2)若把![]() 沿着直线
沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
① 如图2,当点![]() 落在斜边
落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,![]() 与
与![]() 相交于点
相交于点![]() ,如果
,如果![]() ,写出
,写出![]() 与
与![]() 的函数关系式以及定义域.
的函数关系式以及定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
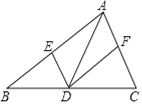
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知抛物线
,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为顶点.
为顶点.
![]() 求直线
求直线![]() 的解析式和顶点
的解析式和顶点![]() 的坐标;
的坐标;
![]() 已知
已知![]() ,点
,点![]() 是直线
是直线![]() 下方的抛物线上一动点,作
下方的抛物线上一动点,作![]() 于点
于点![]() ,当
,当![]() 最大时,有一条长为
最大时,有一条长为![]() 的线段
的线段![]() (点
(点![]() 在点
在点![]() 的左侧)在直线
的左侧)在直线![]() 上移动,首尾顺次连接
上移动,首尾顺次连接![]() 、
、![]() 、
、![]() 、
、![]() 构成四边形
构成四边形![]() ,请求出四边形
,请求出四边形![]() 的周长最小时点
的周长最小时点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 点是线段
点是线段![]() 上一动点,将
上一动点,将![]() 沿直线
沿直线![]() 折叠至
折叠至![]() ,是否存在点
,是否存在点![]() 使得
使得![]() 与
与![]() 重叠部分的图形是直角三角形?若存在,请求出
重叠部分的图形是直角三角形?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
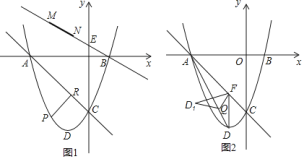
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中日钓鱼岛争端持续,我国海监船加大钓鱼岛海域的巡航维权力度.如图,![]() ,
,![]() 海里,
海里,![]() 海里,钓鱼岛位于
海里,钓鱼岛位于![]() 点,我国海监船在点
点,我国海监船在点![]() 处发现有一不明国籍的渔船自
处发现有一不明国籍的渔船自![]() 点出发沿着
点出发沿着![]() 方向匀速驶向钓鱼岛所在地点
方向匀速驶向钓鱼岛所在地点![]() ,我国海监船立即从
,我国海监船立即从![]() 处出发以相同的速度沿某直线去拦截这艘渔船,结果在点
处出发以相同的速度沿某直线去拦截这艘渔船,结果在点![]() 处截住了渔船.
处截住了渔船.

(1)请用直尺和圆规作出![]() 处的位置.(不写作法,保留作图痕迹)
处的位置.(不写作法,保留作图痕迹)
(2)求我国海监船行驶的航程![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
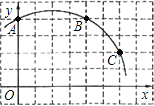
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,MN垂直平分AB分别交AB、BC于M、M,如果△ACN是等腰三角形,那么∠B的大小是______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
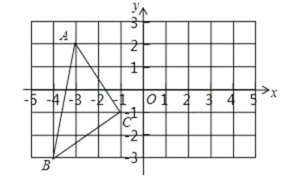
【题目】在平面直角坐标系中,△ABC三个顶点的坐标为:A(﹣3,2),B(﹣4,﹣3)C(﹣1,﹣1)
(1)若△A1B1C1与△ABC关于y轴对称,请写出点A1,B1,C1的坐标(直接写答案):A1 ;B1, ;C1 ;
(2)△ABC的面积为 ;
(3)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com