
【题目】如图中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
(1)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′则三个顶点坐标分别是:A′( , ),B′( , ),C′( , ).
(2)求△ABC的面积.

科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:
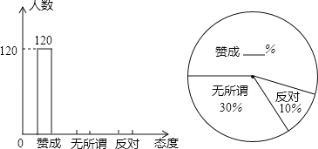
根据上述信息,解答下列问题:
(1)抽取的学生人数为 ;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线互相垂直的四边形
D.对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 18 | 0.12 |
2≤x<3 | a | m |
3≤x<4 | 45 | 0.3 |
4≤x<5 | 36 | n |
5≤x<6 | 21 | 0.14 |
合计 | b | 1 |
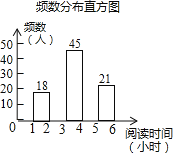
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是权威机构公布的一组反映世界人口的数据:1957年世界人口为30亿,17年后(即1974年)增加了10亿,即达到40亿;又过了13年达到50亿;到1999年全世界人口达到60亿.以此速度,人口学专家预测到2025年,世界人口将达到80亿;而到2050年世界人口将超过90亿,其中亚洲人口最多,将达到52.68亿,北美洲3.92亿,欧洲8.28亿,拉丁美洲及加勒比地区8.09亿,非洲17.68亿.有一位同学根据以上提供的数据制作了三幅统计图,请根据这些统计图回答问题.


(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中最能看出世界人口的总体变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲人口的总和还要多,你从哪幅统计图中可以明显地得到这个结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com