
【题目】若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为 .
【答案】![]() 或
或 ![]()
【解析】解:如图, 
当BF如图位置时,
∵AB=AB,∠BAF=∠ABE=90°,AE=BF,
∴△ABE≌△BAF(HL),
∴∠ABM=∠BAM,
∴AM=BM,AF=BE=3,
∵AB=4,BE=3,
∴AE= ![]() =
= ![]() =5,
=5,
过点M作MS⊥AB,由等腰三角形的性质知,点S是AB的中点,BS=2,SM是△ABE的中位线,
∴BM= ![]() AE=
AE= ![]() ×5=
×5= ![]() ,
,
当BF为BG位置时,易得Rt△BCG≌Rt△ABE,
∴BG=AE=5,∠AEB=∠BGC,
∴△BHE∽△BCG,
∴BH:BC=BE:BG,
∴BH= ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半)的相关知识才是答题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
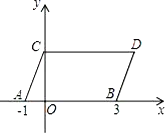
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,.B 的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2) 在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
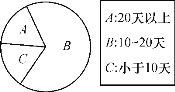
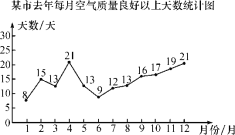
【题目】空气质量状况已引起全社会的广泛关注,某市统计了去年每月空气质量达到良好以上的天数,整理后制成如图所示的折线统计图和扇形统计图.根据以上信息解答下列问题:该市去年空气质量连续提升的月份范围是____;扇形统计图中扇形A的圆心角的度数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
(1)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′则三个顶点坐标分别是:A′( , ),B′( , ),C′( , ).
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知![]() 是
是![]() 外一点,连接
外一点,连接![]() ,求
,求![]() 的度数.
的度数.

解:(1)如图1,过点![]() 作
作![]() ,所以依据
,所以依据![]() ,
,![]() (依据①_____).又因为
(依据①_____).又因为![]() (依据②_____),所以
(依据②_____),所以![]() .
.
填空:①是_______;②是______.
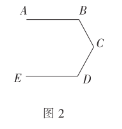
(2)如图2,![]() ,求
,求![]() 的度数.
的度数.
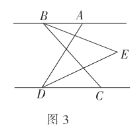
(3)如图3,![]() ,点
,点![]() 在点
在点![]() 的右侧,
的右侧,![]() ;点
;点![]() 在点
在点![]() 的左侧,
的左侧,![]() .
.![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 所在的直线交于点
所在的直线交于点![]() ,点
,点![]() 在
在![]() 与
与![]() 两条平行线之间,求
两条平行线之间,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,BE平分∠ABC.
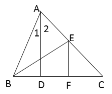
(1)若∠EBC=32°,∠1∶∠2=1∶2,EF∥AD,求∠FEC的度数.
(2)若∠2=50°,点F为射线CB上的一个动点,当△EFC为钝角三角形时,直接写出∠FEC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干人乘坐若干辆汽车,如果每辆汽车坐22人,有1人不能上车;如果有一辆车不坐人,那么所有旅客正好能平分乘到其他各车上,则旅客共________人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com