
【题目】如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离. 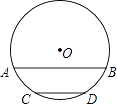
【答案】解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC, ∵AB∥CD,
∴OF⊥CD,
∵AB=30cm,CD=16cm,
∴AE= ![]() AB=
AB= ![]() ×30=15cm,CF=
×30=15cm,CF= ![]() CD=
CD= ![]() ×16=8cm,
×16=8cm,
在Rt△AOE中,
OE= ![]() =
= ![]() =8cm,
=8cm,
在Rt△OCF中,
OF= ![]() =
= ![]() =15cm,
=15cm,
∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.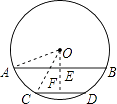
【解析】过点O作弦AB的垂线,垂足为E,延长AE交CD于点F,连接OA,OC;由于AB∥CD,则OF⊥CD,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠BOE=4∶1,则∠AOF等于( )

A. 130°
B. 120°
C. 110°
D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,过点A(8,6)分别做x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
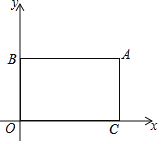
(1)直接写出点B和点C的坐标:B( , )C( , ).
(2)当点P运动时,用含t的代数式表示线段AP的长,并写出t的取范围;
(3)点D(2,0),连结PD、AD,在(2)的条件下是否存在这样的t值,使S△APD=![]() S四边形ABOC,若存在,请求t值,若不存在,请说明理由.
S四边形ABOC,若存在,请求t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a= , ![]() =;
=;
(2)请完成图中表示乙成绩变化情况的折线;
(3)①观察图,可看出的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).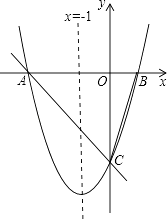
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC , 求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com