练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，直线AB交CD于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠BOE＝4∶1，则∠AOF等于(　　)

    A. 130°

    B. 120°

    C. 110°

    D. 100°

    【答案】B

    【解析】

    先设出∠BOE=α，再表示出∠DOE=α∠AOD=4α，建立方程求出α，最用利用对顶角，角之间的和差即可．

    解：设∠BOE=α，
    ∵∠AOD：∠BOE=4：1，
    ∴∠AOD=4α，
    ∵OE平分∠BOD，
    ∴∠DOE=∠BOE=α
    ∴∠AOD+∠DOE+∠BOE=180°，
    ∴4α+α+α=180°，
    ∴α=30°，
    ∴∠AOD=4α=120°，
    ∴∠BOC=∠AOD=120°，
    ∵OF平分∠COB，
    ∴∠COF=∠BOC=60°，
    ∵∠AOC=∠BOD=2α=60°，
    ∴∠AOF=∠AOC+∠COF=120°，
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（11·西宁）（本小题满分7分）给出三个整式a2，b2和2ab．

    （1）当a＝3，b＝4时，求a2＋b2＋2ab的值；

    （2）在上面的三个整式中任意选择两个整式进行加法或减法运算，使所得的多项式能够因式分解．请写也你所选的式子及因式分解的过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，剪两张对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠BOC＝60°，OF平分∠BOC.若AO⊥BO，OE平分∠AOC，则∠EOF的度数是(　　)

    A. 45°

    B. 15°

    C. 30°或60°

    D. 45°或15°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

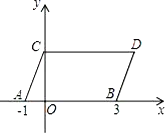
    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(﹣1，0)，(3，0)，现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，.B 的对应点C，D，连接AC，BD，CD.

    (1)求点C，D的坐标及四边形ABDC的面积S四边形ABDC；

    (2) 在y轴上是否存在一点P，连接PA，PB，使S三角形PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

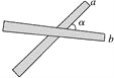
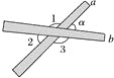
    【题目】如图，取两根木条a、b，将它们钉在一起，并把它们想象成两条直线，就得到一个相交线的模型．你能说出其中的一些邻补角与对顶角吗？两根木条所成的角中，如果∠α＝35°，其它三个角各等于多少度？如果∠α等于90°，115°，m°呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

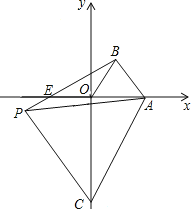
    【题目】如图，在平面直角坐标系中，点A的坐标是（a，0）（a＞0），点C是y轴上的一个动点，点C在y轴上移动时，始终保持△ACP是等边三角形，当点C移动到点O时，得到等边△AOB（此时点P与点B重合）．

    （1）点C在移动的过程中，当等边三角形ACP的顶点P在第三象限时（如图所示），求证：△AOC≌△ABP；

    （2）若点P在第三象限，BP交x轴于点E，且∠ACO＝20°，求∠PAE的度数和E点的坐标；

    （3）若∠APB＝30°，则点P的横坐标为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰直角△ABC，点P是斜边BC上一点（不与B，C重合），PE是△ABP的外接圆⊙O的直径

    （1）求证：△APE是等腰直角三角形；
    （2）若⊙O的直径为2，求 的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的半径为17cm，弦AB∥CD，AB=30cm，CD=16cm，圆心O位于AB，CD的上方，求AB和CD的距离．

    查看答案和解析>>

    同步练习册答案