
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЪЧЃЈaЃЌ0ЃЉЃЈaЃО0ЃЉЃЌЕуCЪЧyжсЩЯЕФвЛИіЖЏЕуЃЌЕуCдкyжсЩЯвЦЖЏЪБЃЌЪМжеБЃГжЁїACPЪЧЕШБпШ§НЧаЮЃЌЕБЕуCвЦЖЏЕНЕуOЪБЃЌЕУЕНЕШБпЁїAOBЃЈДЫЪБЕуPгыЕуBжиКЯЃЉЃЎ
ЃЈ1ЃЉЕуCдквЦЖЏЕФЙ§ГЬжаЃЌЕБЕШБпШ§НЧаЮACPЕФЖЅЕуPдкЕкШ§ЯѓЯоЪБЃЈШчЭМЫљЪОЃЉЃЌЧѓжЄЃКЁїAOCЁеЁїABPЃЛ
ЃЈ2ЃЉШєЕуPдкЕкШ§ЯѓЯоЃЌBPНЛxжсгкЕуEЃЌЧвЁЯACOЃН20ЁуЃЌЧѓЁЯPAEЕФЖШЪ§КЭEЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєЁЯAPBЃН30ЁуЃЌдђЕуPЕФКсзјБъЮЊЁЁ ЁЁЃЎ
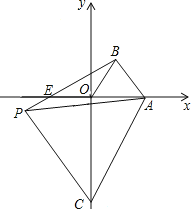
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЁЯPAEЃНЁЯOACЉЁЯCAPЃН10ЁуЃЌEЃЈЉaЃЌ0ЃЉЃЛЃЈ3ЃЉЉaЛђ2aЃЎ
ЁОНтЮіЁП
(1) ЯШХаЖЯГіЁЯOAC=ЁЯBAP, НјЖјЕУГіНсТл;
(2) РћгУжБНЧШ§НЧаЮЕФаджЪЕУГіЁЯOAC, НјЖјЕУГіЁЯPAE, дйРћгУШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯAPB,РћгУШ§НЧаЮЕФЭтНЧЕУГіЁЯAEB=30![]() , МДПЩЕУГіНсТл;
, МДПЩЕУГіНсТл;
(3) ЗжЕуCдкyжсИКАыжсКЭе§АыжсЩЯ,ХаЖЯГіЕуPдкxжсЩЯ, МДПЩЕУГіНсТл.
ЃЈ1ЃЉжЄУїЃКЁпЁїAOBКЭЁїACPЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрOAЃНABЃЌAPЃНACЃЌЁЯOABЃНЁЯCAPЃН60Ёу
ЁрЁЯOACЃНЁЯBAPЃЌ
дкЁїAOCКЭЁїABPжаЃЌ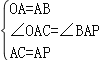 ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїABPЃЈSASЃЉЃЌ
ЃЈ2ЃЉНтЃКЁпЁЯACOЃН20ЁуЃЌ
ЁрЁЯOACЃН90ЁуЉ20ЁуЃН70ЁуЃЌ
ЁпЁЯCAPЃН60ЁуЃЌ
ЁрЁЯPAEЃНЁЯOACЉЁЯCAPЃН10ЁуЃЛ
гЩЃЈ1ЃЉжЊЃЌЁїAOCЁеЁїABPЃЌ
ЁрЁЯABPЃНЁЯAOCЃН90ЁуЃЌЁЯACOЃНЁЯAPBЃН20ЁуЃЌ
ЁрЁЯAEBЃНЁЯAPB+ЁЯPAEЃН20Ёу+10ЁуЃН30ЁуЃЌ
ЁпAЃЈaЃЌ0ЃЉЃЌ
ЁрOAЃНaЃЌ
ЁрABЃНOAЃНaЃЌ
дкRtЁїABEжаЃЌAEЃН2ABЃН2aЃЌ
ЁрOEЃНAEЉOAЃНaЃЌ
ЁрEЃЈЉaЃЌ0ЃЉЃЛ
ЃЈ3ЃЉ
ЕБЕуCдкyжсИКАыжсЩЯЪБЃЌЕБЁЯAPBЃН30ЁуЪБЃЌ
гЩЃЈ1ЃЉжЊЃЌЁїAOCЁеЁїABPЃЌ
ЁрЁЯABPЃНЁЯAOCЃН90ЁуЃЌ
ЁпЁЯOABЃН60ЁуЃЌ
ЁрЁЯAEBЃН30ЁуЃНЁЯAPBЃЌ
ЁрЕуPКЭЕуEжиКЯЃЌ
МДЃКЕуPдкxжсЩЯЃЌ
дкRtЁїABEжаЃЌABЃНaЃЌ
ЁрAPЃН2ABЃН2aЃЌ
ЁрOPЃНAPЉOAЃНaЃЌ
ЁрPЃЈЉaЃЌ0ЃЉЃЛ
ЕБЕуCдкyжсе§АыжсЪБЃЌ
ШчЭМЃЈзЂЃКЮЊСЫЫЕУїЕуPвВдкxжсЩЯЃЌзїЕФЭМаЮЃЌВЛБъзМЃЉ
ЁпЁЯAOBЃН60ЁуЃЌ
ЁрЁЯAPBЃН![]() ЁЯAOBЃЌ
ЁЯAOBЃЌ
ЁрЕуPдквдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЩЯЃЌ
ЁрOPЃНOAЃЌ
дкЁїAOCКЭЁїPOCжаЃЌ ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїPOCЃЌ
ЁрЁЯACOЃНЁЯPCOЃЌ
ЁпЁЯACPЃН60ЁуЃЌ
ЁрЁЯACOЃНЁЯPCOЃЌ
ЁрOCЁЭAPЃЌ
ЁпOCЁЭOAЃЌЁрЕуPдкxжсЩЯЃЌ
ЁрЕуPЕФКсзјБъЮЊЉaЃЌ
ЕБЕуCдкyжсАыжсЩЯЪБЃЌЁЯAPBЃН30ЁуЃЌШчЭМ1ЃЌЃЈзЂЃКЮЊСЫЫЕУїЕуBКЭFжиКЯЃЌзїЕФЭМаЮЃЌВЛБъзМЃЉ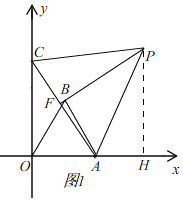
гЩЃЈ1ЃЉжЊЃЌЁїAOCЁеЁїABPЃЈSASЃЉЃЌ
ЁрЁЯABPЃНЁЯOACЃН90ЁуЃЌ
ЁпдкЕШБпШ§НЧаЮACPжаЃЌЁЯCAPЃН60ЁуЃЌ
ЁпЁЯAPBЃН30ЁуЃЌ
ЁрЁЯAFPЃН90ЁуЃЌ
ЁрЕуBКЭFжиКЯЃЌ
ЁрABЃН![]() ACЃН
ACЃН![]() APЃЌ
APЃЌ
ЁпOAЃНABЃЌ
ЁрOAЃН![]() APЃЌ
APЃЌ
Й§ЕуPзїPHЁЭOAгкHЃЌ
ЁрЁЯPAHЃН60ЁуЃЌ
ЁрAHЃН![]() APЃЌ
APЃЌ
ЁрAHЃНOAЃЌ
ЁрAHЃН2OAЃЌ
ЁпAЃЈaЃЌ0ЃЉЃЌ
ЁрOAЃНaЃЌ
ЁрAHЃН2aЃЌ
ЁрЕуPЕФКсзјБъЮЊ2aЃЌ
ЙЪД№АИЮЊЃКЉaЛђ2aЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOЮЊжБЯпABЩЯвЛЕуЃЌЁЯAOCЃН50ЁуЃЌODЦНЗжЁЯAOCЃЌЁЯDOEЃН90Ёу.
(1)ЧыФуЪ§вЛЪ§ЃЌЭМжагаЖрЩйИіаЁгкЦННЧЕФНЧЃЛ
(2)ЧѓГіЁЯBODЕФЖШЪ§ЃЛ
(3)ЧыЭЈЙ§МЦЫуЫЕУїOEЪЧЗёЦНЗжЁЯBOC.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=3cmЃЌBC=6cm.ЕуPДгЕуDГіЗЂЯђЕуAдЫЖЏЃЌдЫЖЏЕНЕуAМДЭЃжЙЃЛЭЌЪБЃЌЕуQДгЕуBГіЗЂЯђЕуCдЫЖЏЃЌдЫЖЏЕНЕуCМДЭЃжЙЃЌЕуPЁЂQЕФЫйЖШЖМЪЧ1cm/s.СЌНгPQЁЂAQЁЂCP.ЩшЕуPЁЂQдЫЖЏЕФЪБМфЮЊts.
ЕБtЮЊКЮжЕЪБЃЌЫФБпаЮABQPЪЧОиаЮЃЛ
ЕБtЮЊКЮжЕЪБЃЌЫФБпаЮAQCPЪЧСтаЮЃЛ
ЗжБ№ЧѓГіЃЈ2ЃЉжаСтаЮAQCPЕФжмГЄКЭУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌжБЯпABНЛCDгкЕуOЃЌOEЦНЗжЁЯBODЃЌOFЦНЗжЁЯCOBЃЌЁЯAODЁУЁЯBOEЃН4ЁУ1ЃЌдђЁЯAOFЕШгк(ЁЁЁЁ)

A. 130Ёу
B. 120Ёу
C. 110Ёу
D. 100Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУБпГЄЯрЕШЕФЯТСаСНжже§ЖрБпаЮЃЌВЛФмНјааЦНУцЯтЧЖЕФЪЧЃЈЁЁЁЁЃЉ
A. ЕШБпШ§НЧаЮКЭе§СљБпаЮ B. е§ЗНаЮКЭе§АЫБпаЮ
C. е§ЮхБпаЮКЭе§ЪЎБпаЮ D. е§СљБпаЮКЭе§ЪЎЖўБпаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЁЯMON=80ЁуЃЌOEЦНЗжЁЯMONЃЌЕуAЁЂBЁЂCЗжБ№ЪЧЩфЯпOMЁЂOEЁЂONЩЯЕФЖЏЕуЃЈAЁЂBЁЂCВЛгыЕуO жиКЯЃЉЃЌСЌНгACНЛЩфЯпOEгкЕуDЃЎЩшЁЯOAC=xЁуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєABЁЮONЃЌдђЃКЂйЁЯABOЕФЖШЪ§ЪЧЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЂкШчЭМ2ЃЌЕБЁЯBAD=ЁЯABDЪБЃЌЪдЧѓxЕФжЕЃЈвЊЫЕУїРэгЩЃЉЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌШєABЁЭOMЃЌдђЪЧЗёДцдкетбљЕФXЕФжЕЃЌЪЙЕУЁїADBжагаСНИіЯрЕШЕФНЧЃПШєДцдкЃЌжБНгаДГіxЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎЃЈздМКЛЭМЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁѕABCDжаЃЌOЪЧACЁЂBDЕФНЛЕуЃЌЙ§ЕуO гыACДЙжБЕФжБЯпНЛБпADгкЕуEЃЌШєЁѕABCDЕФжмГЄЮЊ22cmЃЌдђЁїCDEЕФжмГЄЮЊЃЈ ЃЉЃЎ
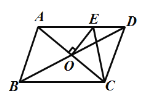
A. 8cm B. 10cm C. 11cm D. 12cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌжБНгаДГі![]() ЕФЪ§СПЙиЯЕЮЊ ЃЛ
ЕФЪ§СПЙиЯЕЮЊ ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌ![]() гы
гы![]() ЕФНЧЦНЗжЯпЫљдкЕФжБЯпЯрНЛгкЕу
ЕФНЧЦНЗжЯпЫљдкЕФжБЯпЯрНЛгкЕу![]() ЃЌЪдЬНОП
ЃЌЪдЬНОП![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
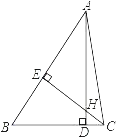
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌADЁЭBCЃЌCEЁЭABЃЌДЙзуЗжБ№ЮЊDЁЂEЃЌADЁЂCEНЛгкЕуHЃЌЧыФуЬэМгвЛИіЪЪЕБЕФЬѕМўЃК_____ЃЌЪЙЁїAEHЁеЁїCEBЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com