
【题目】如图,抛物线y=﹣ ![]() x2+bx+c经过A(﹣1,0),B(0,2)两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B′,点A落到点A′的位置.
x2+bx+c经过A(﹣1,0),B(0,2)两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B′,点A落到点A′的位置.
(1)求抛物线对应的函数关系式;
(2)将抛物线沿y轴平移后经过点A′,求平移后所得抛物线对应的函数关系式;
(3)设(2)中平移后所得抛物线与y轴的交点为C,若点P在平移后的抛物线上,且满足△OCP的面积是△O′A′P面积的2倍,求点P的坐标;
(4)设(2)中平移后所得抛物线与y轴的交点为C,与x轴的交点为D,点M在x轴上,点N在平移后所得抛物线上,直接写出以点C,D,M,N为顶点的四边形是以CD为边的平行四边形时点N的坐标.
【答案】
(1)
解:如图1,把A(﹣1,0),B(0,2)两点坐标代入y=﹣ ![]() x2+bx+c得:
x2+bx+c得:
 ,
,
解得: ![]() ,
,
∴抛物线对应的函数关系式:y=﹣ ![]() x2+
x2+ ![]() x+2
x+2

(2)
解:如图2,∵A(﹣1,0),B(0,2),
∴OA=1,OB=2,
由旋转得:O′B=OB=2,O′A′=OA=1,且旋转角∠OBO′=90°,
∴O′(2,2),A′(2,1),
所以由原抛物线从O′平移到A′可知,抛物线向下平移1个单位,
∴平移后所得抛物线对应的函数关系式:y=﹣ ![]() x2+
x2+ ![]() x+1
x+1

(3)
解:设P(a,﹣ ![]() a2+
a2+ ![]() a+1),
a+1),
y=﹣ ![]() x2+
x2+ ![]() x+1,
x+1,
当x=0时,y=1,
∴OC=A′O′=1,
根据点A(2,2)可分三种情况:
①当a>2时,如图3,

∵S△OCP=2S△O′A′P,
∴ ![]() ×1×a=2×
×1×a=2× ![]() ×1×(a﹣2),
×1×(a﹣2),
a=4,
则y=﹣ ![]() a2+
a2+ ![]() a+1=﹣
a+1=﹣ ![]() ×42+
×42+ ![]() ×4+1=﹣
×4+1=﹣ ![]() ,
,
∴P(4,﹣ ![]() ),
),
②当0<a<2时,如图4,

∵S△OCP=2S△O′A′P,
∴ ![]() ×1×a=2×
×1×a=2× ![]() ×1×(2﹣a),
×1×(2﹣a),
a= ![]() ,
,
则y=﹣ ![]() a2+
a2+ ![]() a+1=﹣
a+1=﹣ ![]() ×
× ![]() 2+
2+ ![]() ×
× ![]() +1=
+1= ![]() ,
,
∴P( ![]() ,
, ![]() ),
),
③当a<0时,如图5,

同理得: ![]() ×1×(﹣a)=2×
×1×(﹣a)=2× ![]() ×(﹣a+2),
×(﹣a+2),
a=4(不符合题意,舍),
综上所述,点P的坐标为(4,﹣ ![]() )或(
)或( ![]() ,
, ![]() )
)
(4)
解:设N(m,﹣ ![]() m2+
m2+ ![]() m+1),
m+1),
如图6,过N作NE⊥x轴于E,

∵四边形CMND是平行四边形,
∴CD∥MN,CD=MN,
∴∠CDO=∠MEN,
∵∠COD=∠MEN=90°,
∴△COD≌△NEM,
∴EN=CO,
∴ ![]() m2﹣
m2﹣ ![]() m﹣1=1,
m﹣1=1,
解得:m=3或﹣1,
当m=3时,y=﹣1,
当m=﹣1时,y=﹣1,
∴N(3,﹣1)或(﹣1,﹣1),
如图7就是点N(﹣1,﹣1)时,所成的平行四边形;

如图8和如图9,


∵四边形CDMN是平行四边形,
∴CN∥DM,
∴点C与点N是对称点,
∵C(0,1),对称轴是x=﹣  =1,
=1,
∴N(2,1),
综上所述,点N的坐标为(3,﹣1)或(﹣1,﹣1)或(2,1).
【解析】(1)如图1,利用待定系数法求二次函数的关系式;(2)如图2,根据旋转得出点O′(2,2),A′(2,1),知道原抛物线从向下平移1个单位得到新抛物线,根据原抛物线的关系式可以写出新抛物线的函数关系式;(3)设P(a,﹣ ![]() a2+
a2+ ![]() a+1),根据点P的位置和A′的横坐标2可以分为三种情况:①当a>2时,如图3,②当0<a<2时,如图4,③当a<0时,如图5,分别根据S△OCP=2S△O′A′P , 列等式求出a的值,并求出对应P的坐标;(4)如图6,因为点N在平移后所得抛物线上,所以设N(m,﹣
a+1),根据点P的位置和A′的横坐标2可以分为三种情况:①当a>2时,如图3,②当0<a<2时,如图4,③当a<0时,如图5,分别根据S△OCP=2S△O′A′P , 列等式求出a的值,并求出对应P的坐标;(4)如图6,因为点N在平移后所得抛物线上,所以设N(m,﹣ ![]() m2+
m2+ ![]() m+1),作辅助线,构建全等三角形,发现点N的纵坐标的绝对值为1,由此列式为:
m+1),作辅助线,构建全等三角形,发现点N的纵坐标的绝对值为1,由此列式为: ![]() m2﹣
m2﹣ ![]() m﹣1=1,解出m的值,求出点N的坐标.同理如图7得出点N的坐标.
m﹣1=1,解出m的值,求出点N的坐标.同理如图7得出点N的坐标.
如图8和9,点C与点N是对称点,根据点C的坐标求点N的坐标.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣ ![]() ),(
),( ![]() )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 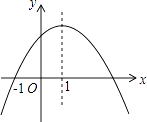
A.①②
B.②③
C.②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图: 
根据上述信息,解答下列问题:
(1)抽取的学生人数为;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
①abc>0;②b2﹣4ac>0;③b=﹣2a;④a+b+c>2,
其中正确的是(填写序号)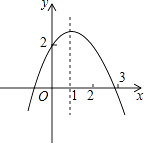
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=4,BD平分∠ABC,过点A作AD⊥BD于点D,过点D作DE∥CB,分別交AB、AC于点E、F,若EF=2DF,则AB的长为( )

A. 4 B. 6 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题与探索
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 . 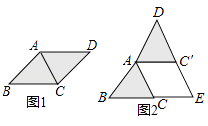
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.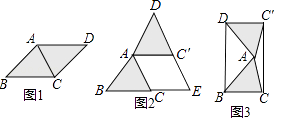
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 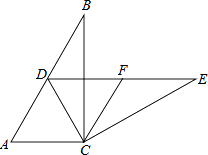
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数对应的点上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com