
【题目】在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,把△ABD沿AD折叠后,使得点B落在点E处,连接CE,若∠DBE=15°,则∠ADC的度数为________
【答案】75°或105°
【解析】
分点E落在直线BC上方和下方两种情况进行讨论求解.
解:当点E在直线BC下方时,如图1所示:
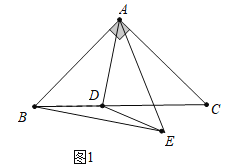
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
根据折叠的性质,可知△ADB≌△ADE,
∴ BD=DE,∠ABD=∠AED=45°,∠DAB=∠DAE,
∴ ∠DBE=∠DEB=15°,
∴∠ABE=∠AEB=∠ABC+∠DBE=45°+15°=60°,
∴∠DAB=![]() (180°-∠ABE -∠AEB)=
(180°-∠ABE -∠AEB)=![]() (180°-60°-60°)=30°,
(180°-60°-60°)=30°,
∴∠ADC=∠ABC+∠DAB =45°+30°=75°.
当点E在直线BC上方时,如图2所示:
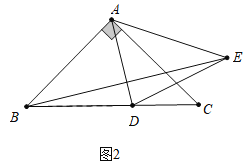
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
根据折叠的性质,可知△ADB≌△ADE,
∴ BD=DE,∠ABD=∠AED=45°,∠DAB=∠DAE,
∴ ∠DBE=∠DEB=15°,
∴∠ABE=∠AEB=∠ABC-∠DBE=45°-15°=30°,
∴∠DAB=![]() (180°-∠ABE -∠AEB)=
(180°-∠ABE -∠AEB)=![]() (180°-30°-30°)=60°,
(180°-30°-30°)=60°,
∴∠ADC=∠ABC+∠DAB =45°+60°=105°.
故答案为:75°或105°.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象过点A(1,1),将其图象沿直线y=x平移到点B(2,2)处,过点作BC⊥x轴,交原图象于点D,则阴影部分(△ABD)的面积为_____.
的图象过点A(1,1),将其图象沿直线y=x平移到点B(2,2)处,过点作BC⊥x轴,交原图象于点D,则阴影部分(△ABD)的面积为_____.
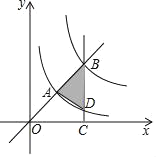
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;并写出A1、B1、C1三点的坐标.
(2)求出(1)中C点旋转到C1点所经过的路径长(结果保留π).
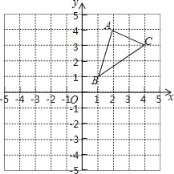
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
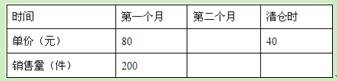
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16,AD是BC边上的中线且AD=6,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).

A.![]() B.16C.6D.10
B.16C.6D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
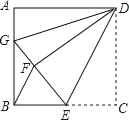
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE,使点B落在点F处,连接AF,则当线段AF的长取最小值时,tan∠FBD是____.
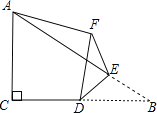
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM、GN是折痕,若正方形EFGH与五边形MCNGF面积相等,则![]() 的值是____________
的值是____________
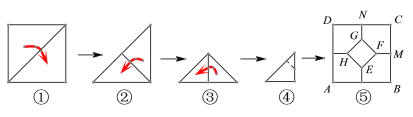
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
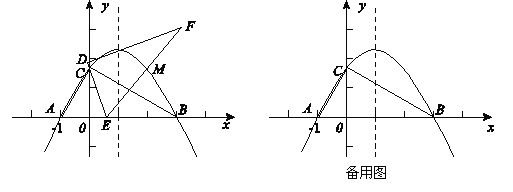
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com