
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
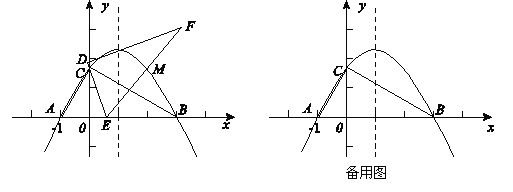
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
【答案】(1)B(3,0),C(0,![]() ),
),![]() (2)①x=2②存在P点坐标为(1,2)或(1,—2)或(1,2
(2)①x=2②存在P点坐标为(1,2)或(1,—2)或(1,2![]() )或(1,
)或(1,![]() )
)
【解析】
解:(1)B(3,0),C(0,![]() )。
)。
∵A(—1,0)B(3,0)
∴可设过A、B、C三点的抛物线为![]() 。
。
又∵C(0,![]() )在抛物线上,∴
)在抛物线上,∴![]() ,解得
,解得![]() 。
。
∴经过A、B、C三点的抛物线解析式![]() 即
即![]() 。
。
(2)①当△OCE∽△OBC时,则![]() 。
。
∵OC=![]() , OE=AE—AO=x-1, OB=3,∴
, OE=AE—AO=x-1, OB=3,∴![]() 。∴x=2。
。∴x=2。
∴当x=2时,△OCE∽△OBC。
②存在点P。
由①可知x=2,∴OE=1。∴E(1,0)。 此时,△CAE为等边三角形。
∴∠AEC=∠A=60°。
又∵∠CEM=60°, ∴∠MEB=60°。
∴点C与点M关于抛物线的对称轴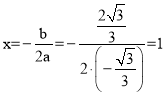 对称。
对称。
∵C(0,![]() ),∴M(2,
),∴M(2,![]() )。
)。
过M作MN⊥x轴于点N(2,0),

∴MN=![]() 。 ∴ EN=1。
。 ∴ EN=1。
∴![]() 。
。
若△PEM为等腰三角形,则:
ⅰ)当EP=EM时, ∵EM=2,且点P在直线x=1上,∴P(1,2)或P(1,-2)。
ⅱ)当EM=PM时,点M在EP的垂直平分线上,∴P(1,2![]() ) 。
) 。
ⅲ)当PE=PM时,点P是线段EM的垂直平分线与直线x=1的交点,∴P(1,![]() )
)
∴综上所述,存在P点坐标为(1,2)或(1,—2)或(1,2![]() )或(1,
)或(1,![]() )时,
)时,
△EPM为等腰三角形。
(1)由已知,根据锐角三角函数定义和特殊角的三角函数值可求出OC和AB的长,从而求得点B、C的坐标。设定交点式,用待定系数法,求得抛物线解析式。
(2)①根据相似三角形的性质,对应边成比例列式求解。
②求得EM的长,分EP=EM, EM=PM和PE=PM三种情况求解即可。


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,把△ABD沿AD折叠后,使得点B落在点E处,连接CE,若∠DBE=15°,则∠ADC的度数为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
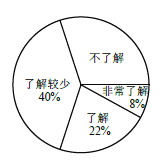

(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
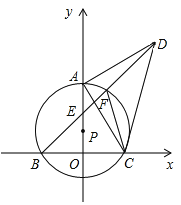
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4![]() ,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,
,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF, ![]() 经过点C,则图中阴影部分的面积为( )
经过点C,则图中阴影部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com