
分析 先列出二次根式相加减的式子,再把各二次根式化为最减二次根式,合并同类项即可.
解答 解:∵一个三角形的三边长分别是$\sqrt{80}$cm、$\sqrt{12}$cm、$\sqrt{18}$cm,
∴这个三角形的周长=$\sqrt{80}$+$\sqrt{12}$+$\sqrt{18}$=(4$\sqrt{5}$+2$\sqrt{3}$+3$\sqrt{2}$)cm.
故答案为:4$\sqrt{5}$+2$\sqrt{3}$+3$\sqrt{2}$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D、E分别是边AB和AC上的点,AD=2BD,DE∥BC,S△ABC=36,则S△ADE=( )
如图,在△ABC中,点D、E分别是边AB和AC上的点,AD=2BD,DE∥BC,S△ABC=36,则S△ADE=( )| A. | 9 | B. | 16 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校对八年级300名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级支持“分组合作学习”方式的学生(含非常喜欢和喜欢两种情况)约为( )
某校对八年级300名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级支持“分组合作学习”方式的学生(含非常喜欢和喜欢两种情况)约为( )| A. | 180名 | B. | 210名 | C. | 240名 | D. | 270名 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
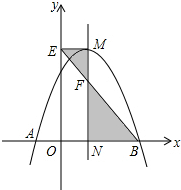 如图,抛物线y=ax2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0),B的坐标为(3,0).
如图,抛物线y=ax2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0),B的坐标为(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com