
 如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.
如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.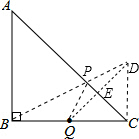
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、正方形的周长C与它的边长a |
| B、除数一定,被除数和商 |
| C、三角形的面积一定,一边的长a与这边上的高h |
| D、每支铅笔0.5元,买铅笔的支数与总的价钱 |
查看答案和解析>>
科目:初中数学 来源: 题型:
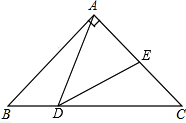 已知如图△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°,△ABD∽△DCE.当△ADE是等腰三角形时,求AE的长.
已知如图△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°,△ABD∽△DCE.当△ADE是等腰三角形时,求AE的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 我国在国际舞台始终注重主动承担国际责任,自2008年12月份起已先后向亚丁湾派出十四批次护航编队,共计四十余艘(次)战舰.2013年6月6日,第十四批护航编队中“微山湖”号综合补给舰从点A处准备靠岸补给休整,然后赶往B点继续执行护航任务,请给出其最佳停靠地点,使其航程最短.
我国在国际舞台始终注重主动承担国际责任,自2008年12月份起已先后向亚丁湾派出十四批次护航编队,共计四十余艘(次)战舰.2013年6月6日,第十四批护航编队中“微山湖”号综合补给舰从点A处准备靠岸补给休整,然后赶往B点继续执行护航任务,请给出其最佳停靠地点,使其航程最短.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | ||
1+
|
1×(
| ||||
(
|
| 2 |
| 1 | ||||
|
1×(
| ||||||||
(
|
| 3 |
| 2 |
| 1 | ||||
|
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com