
【题目】已知:在Rt△ABC中,∠ACB=90°,AB=AC,点D在直线AB上,连接CD,在CD的右侧作CE⊥CD,CD=CE,

(1)如图1,①点D在AB边上,直接写出线段BE和线段AD的关系;
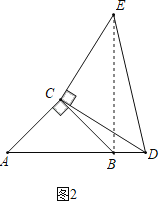
(2)如图2,点D在B右侧,BD=1,BE=5,求CE的长.
(3)拓展延伸
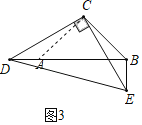
如图3,∠DCE=∠DBE=90,CD=CE,BC=![]() ,BE=1,请直接写出线段EC的长.
,BE=1,请直接写出线段EC的长.
【答案】(1)AD⊥BE;(2)CE=![]() ;(3)CE=
;(3)CE=![]() .
.
【解析】
(1)根据全等三角形的性质得到AD=BE,∠A=∠CBE,求得∠ABE=90°,于是得到结论;
(2)如图2,连接BE,根据全等三角形的性质得到∠A=∠CBE,推出∠DBE=90°,根据勾股定理得到DE=![]() =
=![]() =
=![]() ,即可得到结论;
,即可得到结论;
(3)如图3,过C作CA⊥BC交DB于A,根据已知条件得到D,E,B,C四点共圆,求得∠CDA=∠CEB,根据全等三角形的性质得到AD=BE=1,AC=BC,得到△ACB是等腰直角三角形,于是得到结论.
解:(1)∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠A=∠CBE,
∵∠A+∠ABC=90°,
∴∠ABE=90°,
∴AD⊥BE;
(2)如图2,连接BE,∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴∠A=∠CBE,
∵∠A+∠ABC=90°,
∴∠ABE=90°,
∴∠DBE=90°,
∵BD=1,BE=5,
∴DE=![]() =
=![]() =
=![]() ,
,
∵CD=CE,∠DCE=90°,
∴CE=![]() DE=
DE=![]() ;
;
(3)如图3,过C作CA⊥BC交DB于A,
∵∠DCE=90°,
∴∠DCA=∠ECB,
∵∠DCE=∠DBE=90°,
∴D,E,B,C四点共圆,
∴∠CDA=∠CEB,
∵CD=CE,
∴△CDA≌△CEB(ASA),
∴AD=BE=1,AC=BC,
∴△ACB是等腰直角三角形,
∴AB=![]() BC=2,
BC=2,
∴BD=3,
∴DE=![]() =
=![]() =
=![]() ,
,
∴CE=![]() DE=
DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均毎天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调査表明:这种冰箱的售价毎降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价![]() 元,商场每天销售这种冰箱的利润为
元,商场每天销售这种冰箱的利润为![]() 元,请写出
元,请写出![]() 与
与![]() 间的函数表达式;(不要求写出自变量的取值范围)
间的函数表达式;(不要求写出自变量的取值范围)
(2)商场要想在这种冰箱销售中毎天盈利4800元,同时又要使百姓得到实惠,毎台冰箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线.
(2)若DE+EA=4,⊙O的半径为5,求CF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bc+c的图象如图所示,则下列判断中错误的是( )

A. 图象的对称轴是直线x=﹣1 B. 当x>﹣1时,y随x的增大而减小
C. 当﹣3<x<1时,y<0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
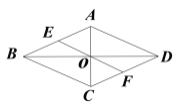
【题目】如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个半径为![]() ,圆心角为
,圆心角为![]() 的扇形
的扇形![]() ,如图放置在直线
,如图放置在直线![]() 上(
上(![]() 与直线
与直线![]() 重合),然后将这个扇形在直线
重合),然后将这个扇形在直线![]() 上无摩擦滚动至
上无摩擦滚动至![]() 的位置,在这个过程中,点
的位置,在这个过程中,点![]() 运动到点
运动到点![]() 的路径长度为( )
的路径长度为( )

A. 4π B. 3π+3 C. 5π D. 5π-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N,动点P在线段BA上以每秒![]() cm的速度由点B向点A运动.同时,动点Q在线段AC上由点N向点C运动,且始终保持MQ⊥MP.一个点到终点时两个点同时停止运动,设运动的时间为t秒(t>0).
cm的速度由点B向点A运动.同时,动点Q在线段AC上由点N向点C运动,且始终保持MQ⊥MP.一个点到终点时两个点同时停止运动,设运动的时间为t秒(t>0).
(1)求证:△PBM∽△QNM.
(2)若∠ABC=60°,AB=4![]() cm,
cm,
①求动点Q的运动速度;
②设△APQ的面积为S(cm2),求S与t的等量关系式(不必写出t的取值范围).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com