
【题目】如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,图中相似的三角形有( )对.
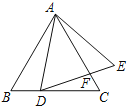
A.3B.4C.5D.6
【答案】C
【解析】
由等边三角形的性质得出∠BAC=∠B=∠C=∠DAE=∠ADE=∠E=60°,得出△ABC∽△ADE,再证出∠BAD=∠FAE,得出△ABD∽△AEF;由∠AFE=∠DFC,∠E=∠C,证出△AEF∽△DCF,得出△ABD∽△DCF;由∠DAF=∠CAD,∠ADF=∠C,即可得出△ADF∽△ACD.
解:图中的相似三角形有△ABC∽△ADE,△ABD∽△AEF,△AEF∽△DCF,△ABD∽△DCF,△ADF∽△ACD;理由如下:
∵△ABC和△ADE均为等边三角形,
∴∠BAC=∠B=∠C=∠DAE=∠ADE=∠E=60°,
∴△ABC∽△ADE;
∵∠BAC=∠DAE,
∴∠BAD=∠FAE,
∴△ABD∽△AEF;
∵∠AFE=∠DFC,∠E=∠C,
∴△AEF∽△DCF,
∴△ABD∽△DCF;
∵∠DAF=∠CAD,∠ADF=∠C,
∴△ADF∽△ACD,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中AB=4, BC=8,点E、F是BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形.
(2)如果四边形AECF是菱形,求这个菱形的边长.
(3)如图2,在(2)的条件下,取AB、CD的中点G、H,连接DG、BH, DG分别交AE、CF于点M、Q, BH分别交AE、CF于点N、P,求点P到BC的距离并直接写出四边形MNPQ的面积。
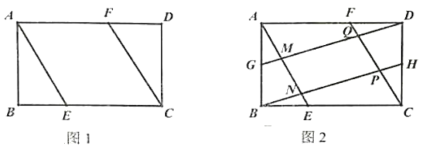
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用铁片制作的圆锥形容器盖如图所示.
(1)我们知道:把平面内线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆.类比圆的定义,给圆锥下定义 ;
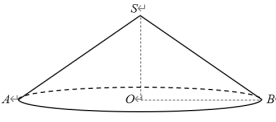
(2)已知OB=2 cm,SB=3 cm,
①计算容器盖铁皮的面积;
②在一张矩形铁片上剪下一个扇形,用它围成该圆锥形容器盖.以下是可供选用的矩形铁片的长和宽,其中可以选择且面积最小的矩形铁片是 .
A.6 cm×4 cm B.6 cm×4.5 cm C.7 cm×4 cm D.7 cm×4.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因抖音等新媒体的传播,西安已成为最著名的网红旅游城市之一,2018年“十一”黄金周期间,接待游客已达![]() 万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗
万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗![]() 元,借鉴以往经验;若每碗小面卖
元,借鉴以往经验;若每碗小面卖![]() 元,平均每天能够销售
元,平均每天能够销售![]() 碗,若降价销售,毎降低
碗,若降价销售,毎降低![]() 元,则平均每天能够多销售
元,则平均每天能够多销售![]() 碗.为了维护城市形象,店家规定每碗小面的售价不得超过
碗.为了维护城市形象,店家规定每碗小面的售价不得超过![]() 元,则当每碗小面的售价定为多少元时,店家才能实现每天盈利
元,则当每碗小面的售价定为多少元时,店家才能实现每天盈利![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,点A1,A2,A3,…都在x轴上,点C1,C2,C3,…都在直线y=![]() x+
x+![]() 上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是__.
上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是__.
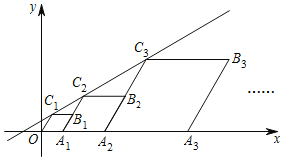
查看答案和解析>>
科目:初中数学 来源: 题型:
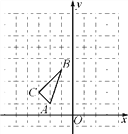
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;
(2)若点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
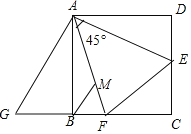
【题目】已知如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF,②BF=![]() ,③AF=
,③AF=![]() ,④S△MEF=
,④S△MEF=![]() 中正确的是
中正确的是![]()
![]()
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
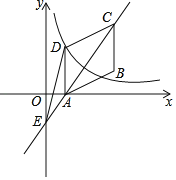
(1)写出D点坐标;
(2)求双曲线的解析式;
(3)作直线AC交y轴于点E,连结DE,求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com