
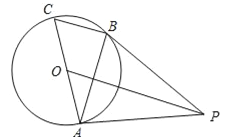
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)连接OB,由圆周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,证出∠PBA+∠OBA=90°,即可得出结论;
(2)证明△ABC∽△PBO,得出对应边成比例,即可求出BC的长.
试题解析:(1)证明:连接OB,如图所示:
∵AC是⊙O的直径,∴∠ABC=90°,∴∠C+∠BAC=90°,∵OA=OB,∴∠BAC=∠OBA,∵∠PBA=∠C,∴∠PBA+∠OBA=90°,即PB⊥OB,∴PB是⊙O的切线;
(2)解:∵⊙O的半径为![]() ,∴OB=
,∴OB=![]() ,AC=
,AC=![]() ,∵OP∥BC,∴∠C=∠BOP,又∵∠ABC=∠PBO=90°,∴△ABC∽△PBO,∴
,∵OP∥BC,∴∠C=∠BOP,又∵∠ABC=∠PBO=90°,∴△ABC∽△PBO,∴![]() ,即
,即![]() ,∴BC=2.
,∴BC=2.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】设一次函数y=kx+2k-3(k≠0),对于任意两个k的值k1,k2,分别对应两个一次函数值y1,y2,若k1k2<0,当x=m时,取相应y1,y2,中的较小值p,则p的最大值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( ) 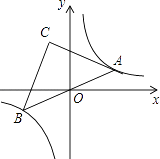
A.y= ![]()
B.y= ![]()
C.y=﹣ ![]()
D.y=﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月份某周,我市每天的最高气温(单位:℃)12,9,10,6,11,12,17,则这组数据的中位数与极差分别是( )
A.8,11B.8,17C.11,11D.11,17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com