Question

5．如图1，AB是⊙O的直径，以OA为直径作半圆O₁，OB为直径作半圆O₂，E是半圆O₁上的一个动点（点E与点A，O不重合），连接AE并延长，交⊙O于点C，连接CO并延长，交⊙O与点D，连接BD交半圆于点O₂于点F，OA=4．
（1）试判断AE与DF的数量关系，并说明理由；
（2）当OC与半圆O₁相切时，求AE的长；
（3）过点C作CG⊥QB，垂足为G，如图2所示，设BF=x，OG=y，求y与x之间的函数关系式，并写出x的取值范围．

Answer 1

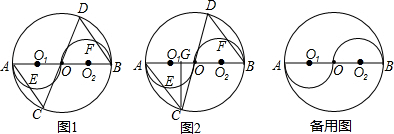
分析 （1）连接OE，OF，得到OE⊥AC，推出AOC≌△BOD，根据全等三角形的性质得到AC=BD，即可得到结论；
（2）根据切线的性质得到∠AOC=90°，根据等腰直角三角形的性质得到∠AOE=45°，由勾股定理即可得到结论；
（3）连接OF，①当点G在OA上时，根据相似三角形的性质得到$\frac{AG}{AC}$=$\frac{BF}{OB}$，于是求得y=-$\frac{1}{2}$x²+4（0＜x≤2$\sqrt{2}$），②当点G在OB上时，根据相似三角形的性质得到于是求得y=x²-4（2$\sqrt{2}$＜x＜4）．

解答 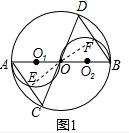解：（1）AE=DF，
证明：如图1，连接OF，
∴OE⊥AC，
∵OA=OAC，
∴AE=CE，
同理可得BF=DF，
在△AOC和△BOD中，$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$，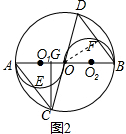
∴AOC≌△BOD，
∴AC=BD，
∴AE=DF；

（2）当OC与半圆O₁相切时，∠AOC=90°，
∴∠AOE=45°，
∵∠OEA=90°，OA=4，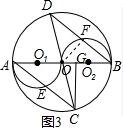
∴AE=2$\sqrt{2}$；

（3）如图2，连接OF，
①当点G在OA上时，由（1）得∠CAG=∠OBF，
∵∠AGC=∠BFO，
∴△AGC∽△BPO，
∴$\frac{AG}{AC}$=$\frac{BF}{OB}$，
即$\frac{4-y}{2x}$=$\frac{x}{4}$，
∴y=-$\frac{1}{2}$x²+4（0＜x≤2$\sqrt{2}$），
②如图3，当点G在OB上时，同①可得△AGC∽△BFO，
∴$\frac{AG}{AC}$=$\frac{BF}{OB}$，
即$\frac{4+y}{2x}=\frac{x}{4}$，
∴y=x²-4（2$\sqrt{2}$＜x＜4）．

点评 本题考查了全等三角形的判定和性质，切线的性质，等腰直角三角形的性质，相似三角形的判定和性质，求函数的解析式，正确的作出辅助线是解题的关键．