
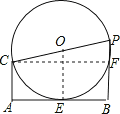
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .

【答案】![]() .
.
【解析】
试题分析:首先判断当AB与⊙O相切时,PB的值最大,设AB与⊙O相切于E,连接OE,则OE⊥AB,过点C作CF⊥PB于F,由CA⊥AB,DB⊥AB,得到AC∥OE∥PB,四边形ABPC是矩形,证得CF=AB=6,在直角三角形PCF中,由勾股定理列方程求解.
试题解析:当AB与⊙O相切时,PB的值最大,
如图,设AB与⊙O相切于E,连接OE,则OE⊥AB,
过点C作CF⊥PB于F,
∵CA⊥AB,DB⊥AB,
∴AC∥OE∥PB,
四边形ABPC是矩形,
∴CF=AB=6,
∵CO=OP,
∴AE=BE,
设PB=x,则PC=2OE=2+x,PF=x-2,
∴(x+2)2=(x-2)2+62,
解得;x=![]() ,
,
∴BP最大值为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在第1个![]() 中,
中,![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第2个
,得到第2个![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第3个
,得到第3个![]() …按此做法继续下去,则第
…按此做法继续下去,则第![]() 个三角形中以
个三角形中以![]() 为顶点的底角度数是( )
为顶点的底角度数是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
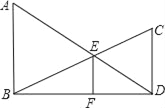
【题目】已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明![]() 成立(不要求考生证明).
成立(不要求考生证明).
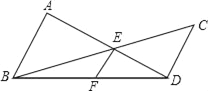
若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:
(1)![]() 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别与正方形
分别与正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 重合.
重合.
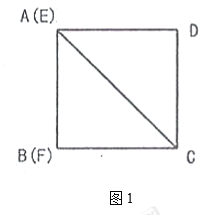
(1)若正方形的边长为![]() ,用含
,用含![]() 的代数式表示:正方形
的代数式表示:正方形![]() 的周长等于_______,
的周长等于_______,![]() 的面积等于_______.
的面积等于_______.
(2)如图2,将![]() 绕点
绕点![]() 顺时针旋转,边
顺时针旋转,边![]() 和正方形的边
和正方形的边![]() 交于点
交于点![]() .连结
.连结![]() ,设旋转角
,设旋转角![]() .
.

①试说明![]() ;
;
②若![]() 有一个内角等于
有一个内角等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“格子乘法”是15世纪中叶,意大利数学家帕乔利在《算术几何及比例性质摘要》一书中介绍的一种两个数的相乘的计算方法.这种方法传入中国之后,在明朝数学家程大位的《算法统宗》书中被称为“铺地锦”具体步骤如下:
①先画一个矩形,把它分成p×q个方格(p,q分别为两乘数的位数)在方格上边、右边分别写下两个因数;
②再用对角线把方格一分为二,分别记录上述各位数字相应乘积的十位数与个位数;
③然后这些乘积由右下到左上,沿对角线方向相加,相加满十时向前进一;
④最后得到结果(方格左侧与下方数字依次排列).比如:
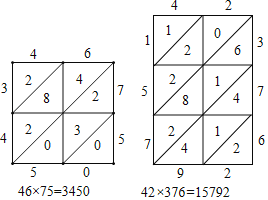
(1)图1是用“铺地锦”计算x9×784的格子,则z= ,x9×784=
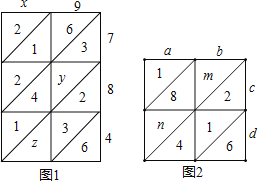
(2)图2是用“铺地锦”计算ab×cd的格子,已知ab×cd=2176,求m和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示数1、![]() .
.

(1)求![]() 的取值范围;
的取值范围;
(2)请你判断数轴上表示数![]() 的点应落在____________,并说明理由.
的点应落在____________,并说明理由.
A.点A的左边 B.线段AB上 C.点B的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
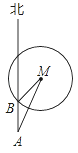
【题目】如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为( )
A. (![]() ﹣1)小时 B. (
﹣1)小时 B. (![]() +1)小时 C. 2小时 D.
+1)小时 C. 2小时 D. ![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新知探究: 光在反射时,光束的路径可用图(1)来表示. ![]() 叫做入射光线,
叫做入射光线,![]() 叫做反射光线,从入射点
叫做反射光线,从入射点![]() 引出的一条垂直于镜面
引出的一条垂直于镜面![]() 的射线
的射线![]() 叫做法线.
叫做法线. ![]() 与
与![]() 的夹角
的夹角![]() 叫入射角,
叫入射角,![]() 与
与![]() 的夹角
的夹角![]() 叫反射角.根据科学实验可得:
叫反射角.根据科学实验可得:![]() .则图(1)中
.则图(1)中![]() 与
与![]() 的数量关系是: 理由: ;
的数量关系是: 理由: ;
问题解决: 生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”![]() 射入到平面镜
射入到平面镜![]() 上、被
上、被![]() 反射到平面镜
反射到平面镜![]() 上,又被平面镜
上,又被平面镜![]() 反射后得到反射光线
反射后得到反射光线![]() .
.
(1)若反射光线![]() 沿着入射光线
沿着入射光线![]() 的方向反射回去,即
的方向反射回去,即![]() ,且
,且![]() ,则
,则![]()
![]()
![]() ;
;
(2)猜想:当![]()
![]() 时,任何射到平面镜
时,任何射到平面镜![]() 上的光线
上的光线![]() 经过平面镜
经过平面镜![]() 和
和![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 总是平行的.请你根据所学过的知识及新知说明.
总是平行的.请你根据所学过的知识及新知说明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com