
����Ŀ�������ϵ�A��Ӧ����Ϊa����B��Ӧ����Ϊb���Ҷ���ʽ6x3y��2xy��5�Ķ�����ϵ��Ϊa��������Ϊb
(1) ֱ��д����a��__________��b��_________
(2) �����ϵ�P��Ӧ����Ϊx����PA��PB��20����x��ֵ
(3) ����M�ӵ�A��������ÿ��1����λ���ȵ��ٶ������������ƶ���ͬʱ��N�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������ƶ�������A����������ز����Ҽ����ƶ������������M��N�������1����λ����
���𰸡���1����1��a����2��b��5����2��x����8.5��11.5����3��2���![]() ���6���8��
���6���8��
��������
��1�����ݶ���ʽ��ϵ�����ɵó����ۣ�
��2����������ۣ�����P�ڵ�A���ʱ������P�ڵ�A�ұ�ʱ���ڵ�B��ߣ��Լ�����P�ڵ�B�ұ�ʱ����������ֱ���⼴�� ��
��3���ֵ�Nδ�����A֮ǰ��֮����������⼴�ɵó����ۣ�
��1���߶���ʽ6x3y-2xy+5�Ķ�����ϵ��Ϊa��������Ϊb��
��a=-2��b=5��
�ʴ�Ϊ��-2��5��
��2���ٵ���P�ڵ�A�������PA+PB=20��: (��2 ��x )+(5��x)=20, ��![]()
�ڵ���P�ڵ�A�ұߣ��ڵ�B�������PA+PB=20��: x ������2 ��+(5��x)=20,
��![]() ��������
��������
�۵���P�ڵ�B�ұ�����PA+PB=20��:x ������2 ��+(x��5), ��![]() .
.
��![]() ��11.5��
��11.5��
��3���辭��t���M��N�������1����λ���ȣ�
���˶�֪��AM��t��BN��2t��
�� ����N�����A֮ǰʱ��
��M��N����ǰ��M��N�������1����λ���ȣ�
t��1��2t��5��2��
���ԣ�t��2�룬
��M��N������M��N�������1����λ���ȣ�
t��2t��1��5��2��
���ԣ�t��![]() �룬
�룬
�� ����N�����A֮��ʱ��
��Nδ��Mʱ��M��N�������1����λ���ȣ�
t��[2t����5��2��]��1��
���ԣ�t��6�룻
��N��M��ʱ��M��N�������1����λ���ȣ�
[2t����5��2��]��t��1��
���ԣ�t��8�룻
��������2���![]() ���6���8���M��N�������1����λ���ȣ�
���6���8���M��N�������1����λ���ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊʹ��һ1200��������У��ʱ���Ϻ�����У��������ǰ��ijУ���꼶����ѧ����������У���ͺ���������������飬�����ݵ�������������ͼ������������ͳ��ͼ��
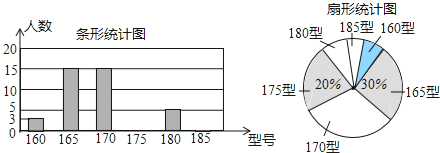
����������Ϣ������������⣺
(1)�ð�ж�����ѧ��?���д�175��У����ѧ���ж���?
(2)������ͳ��ͼ�У���ѿ�ȱ���ֲ���������
(3)������ͳ��ͼ�У������185��У������Ӧ������Բ�ĽǵĴ�С��
(4)��ð�ѧ������У���ͺŵ���������λ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������ѧ����ijУ������һ���ľߴ���Բ����Ϊ��Ʒ����֪����1���ľߴ���2��Բ����21Ԫ������2���ľߴ���3��Բ����39Ԫ��
��1�����ľߴ���Բ��ĵ��ۡ�
��2��ѧУ�������ľߴ�20����Բ�����ɣ��ľߵ���������Żݷ�����
����һ������һ���ľߴ�����1��Բ�档
������������Բ��10������ʱ������10���IJ��ְ�ԭ�۵İ����Żݣ��ľߴ�������.
���蹺�����m������ѡ��һ���ܷ���Ϊ______��ѡ�������ܷ���Ϊ______.
����ѧУ����Բ��100������ѡ�����ַ��������㣿��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ӭ��2018������������ԣ�ij��ѧ��ȫУ���꼶������һ����ѧ�����ԣ��������ȡ�˲���ѧ���IJ��Գɼ���Ϊ�������з��������Ƴ�����������������ͳ��ͼ1��ͼ2���������ͼ����������Ϣ����������⡣
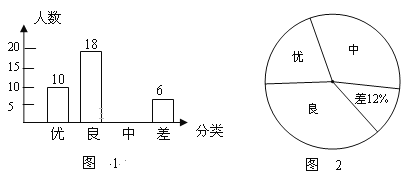
��1���뽫��ʾ�ɼ����Ϊ���С�������ͳ��ͼ����������
��2��������ͳ��ͼ�б�ʾ�ɼ�Ϊ���š����������Ե�Բ�Ľ�Ϊ �ȣ�
��3��ѧУ���꼶����600�˲μ������ѧ���ԣ����Ƹ�У�ж�����ѧ���ɼ����Դﵽ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʮ���굽��֮�ʣ�������ѧ�����ٰ������������������Ϊ����Ķ�����Ϊ��ʹ�����������ԣ�ѧУ��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬Ҫ��ѧ����������.�Ƽ�.����.ũҵ.��ҵ�������鼮�У�ѡȡ�Լ��������һ�֣���ѡ��ֻѡһ�֣���ѧУ���ռ����ĵ������ʵ��������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ�������ͼ����������Ϣ����������⣺
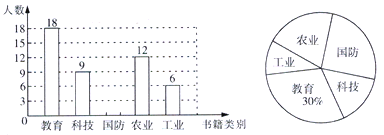
��1������ε����У�һ����ȡ�˶�����ѧ��?
��2����ͨ�����㲹ȫ����ͳ��ͼ��
��3�����������ѧ����1500��ѧ����������Ƹ�У������Ƽ����鼮��ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����д����֤�������е��������ݣ�
��֪����ͼ��ʾ��AC��BD�ཻ��O��DFƽ����CDO��AC�ཻ��F��BEƽ������ABO��AC�ཻ��E����A����C.��֤����1����2.
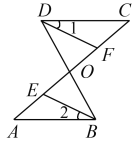
֤�����ߡ�A����C(________)��
��AB��CD (__________________________________)��
���ABO����CDO (__________________________________)��
���ߡ�1��![]() CDO����2��
CDO����2��![]() ��ABO (__________________________________)��
��ABO (__________________________________)��
���1����2(____________________)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չѧ����Ұ���ٽ��鱾֪ʶ������ʵ��������ںϣ�������ij��ѧ��֯���꼶ȫ��ѧ��ǰ�����̛�ˮ��ѧ���ؿ�չ��ѧ����ڴ˴λ�У���ÿλ��ʦ����14��ѧ������ʣ10��ѧ��û��ʦ������ÿλ��ʦ����15��ѧ��������һλ��ʦ�ٴ�6��ѧ�������мס������ִ��Ϳͳ������ǵ��ؿ�������������ʾ��
���Ϳͳ� | ���Ϳͳ� | |
�ؿ�������/���� | 35 | 30 |
���Ԫ/���� | 400 | 320 |
ѧУ�ƻ��˴���ѧ�������ܷ��ò�����3000Ԫ��Ϊ��ȫ�����ÿ���ͳ�������Ҫ��2����ʦ��
��1���μӴ˴���ѧ�����ʦ��ѧ�����ж����ˣ�
��2����Ҫ��֤����ʦ�����г�������Ҫ��֤ÿ����������Ҫ��2����ʦ����֪�������Ϊ�� ������
��3��ѧУ���м��������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
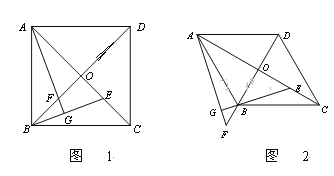
����Ŀ�����ı���ABCD�У��Խ���AC��BD���ڵ�O��E��OC������һ�㣬AG��BE�ڵ�G����BD�ڵ�F��
��1����ͼ1,���ı���ABCD��������,
����֤����AOF�ա�BOE��
������EF,�ж�EF��BC��λ�ù�ϵ����˵�����ɡ�
��2����ͼ2,���ı���ABCD������, ��ABC=1200����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��y����һ��������T���涨��T��x��y��=![]() ������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�����������㣬���磺T��0��1��=
������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�����������㣬���磺T��0��1��=![]() =b��
=b��
��1����֪T��1����1��=��2��T��4��2��=1��
����a��b��ֵ��
��������m�IJ���ʽ��![]() ǡ����3�������⣬��ʵ��p��ȡֵ��Χ��
ǡ����3�������⣬��ʵ��p��ȡֵ��Χ��
��2����T��x��y��=T��y��x��������ʵ��x��y������������T��x��y����T��y��x���������壩����a��bӦ���������Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com