
���Ķ����ϣ��ٽ�����⣺
С��ͬѧ��ѧϰ��Բ�йصĽ�ʱ�˽����ͬԲ���Բ�У�ͬ������Ȼ������Ե�Բ�ܽ���ȣ���ͼ����A��B��C��D��Ϊ��O�ϵĵ㣬���С�C=��D��С�������֣�����E�ڡ�O�⣬�����D��ֱ��ABͬ�࣬���С�D����E��
����ο�С���ó��Ľ��ۣ�����������⣺
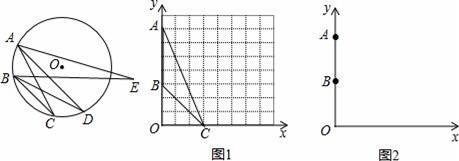

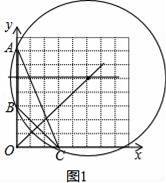
��1����ͼ1����ƽ��ֱ������ϵxOy�У���A������Ϊ��0��7������B������Ϊ��0��3������C������Ϊ��3��0����
����ͼ1��������ABC�����Բ��������Ҫ����ͼ�ۼ�����д��������
������x�������������һ��D���ҡ�ACB=��ADB�����D������Ϊ��������������
��2����ͼ2����ƽ��ֱ������ϵxOy�У���A������Ϊ��0��m������B������Ϊ��0��n��������m��n��0����PΪx���������ϵ�һ�����㣬����APB�ﵽ���ʱ��ֱ��д����ʱ��P�����꣮
��
�����㡿Բ���ۺ��⣮
����������1����������ABC�����ߵ��д��ߵĽ��㣬����ȷ��Բ�ģ������Բ����������
��D���Ǣ���������Բ��x���������Ľ��㣬������ͼд�����꼴�ɣ�
��2������ABΪ�ҵ�Բ��x������������ʱ����Ӧ�ġ�APB����ݴ����������ɶ���������⣮
����𡿽⣺��1����

�ڸ���ͼ�οɵã���D�������ǣ�7��0����
��2������ABΪ�ҵ�Բ��x������������ʱ����CD��y�ᣬ����CP��CB��
��A��������0��m������B��������0��n����
��D�������ǣ�0��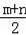
 ������BC=PC=
������BC=PC=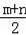
 ��
��
��ֱ�ǡ�BCD�У�BC=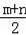
 ��BD=
��BD=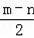
 ��
��
��CD=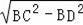
 =
=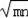
 ��
��
��OP=CD=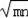
 ��
��
��P�������ǣ�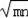
 ��0����
��0����
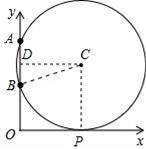

�����������⿼���˴��������Լ����ɶ�������ȷ�����ABΪ�ҵ�Բ��x������������ʱ����Ӧ�ġ�APB����ǹؼ���
��


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��һ���ⳤΪ4cm����������ӣ�һֻ������D1C1���е�M��������BB���е�N�����·���ǣ� ��
A��8 B��2 C��2
C��2 D��2+2
D��2+2

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪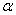 Ϊ��ǣ���
Ϊ��ǣ��� tan(
tan(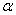 +100)=1,��
+100)=1,��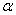 �Ķ���Ϊ�� ����
�Ķ���Ϊ�� ����
A��30�� B��45�� C��20�� D��35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ʵ��
 ��0��
��0��
 ��
��
 ��
��
 ��0.101001000 1����ÿ����1֮�����ζ�1��0���У��������ĸ����ǣ�������
��0.101001000 1����ÿ����1֮�����ζ�1��0���У��������ĸ����ǣ�������
A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��P��˫����y=
 ��x��0����һ����֧�ϵ�һ�㣬�Ե�PΪԲ�ģ�1����λ����Ϊ�뾶����P������P��ֱ��y=3����ʱ����P������Ϊ��������������
��x��0����һ����֧�ϵ�һ�㣬�Ե�PΪԲ�ģ�1����λ����Ϊ�뾶����P������P��ֱ��y=3����ʱ����P������Ϊ��������������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪EF�ǡ�O��ֱ�����ѡ�AΪ60���ֱ�����ǰ�ABC��һ��ֱ�DZ�BC����ֱ��EF�ϣ�б��AB���O���ڵ�P����B���O�غϣ���AC����OE�������ǰ�ABC��OE����ƽ�ƣ�ʹ�õ�B���E�غ�Ϊֹ�����POF=x����x��ȡֵ��Χ�ǣ�������


A��30��x��60 B��30��x��90 C��30��x��120 D��60��x��120
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���� ��
�� �У���֪
�У���֪ ��
�� ��������һ����������ʹ
��������һ����������ʹ �����в������ӵ������ǣ� ��
�����в������ӵ������ǣ� ��
A�� B��
B�� C��
C�� D��
D��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com