
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A����Ϊ����4��4������B������Ϊ��4��0����
��1����ֱ��AB�Ľ���ʽ��
��2����M���������ϵ�һ���㣬��ABΪֱ�DZ߹���ֱ�������Ρ�ABM��������������������е�M�����ꣻ
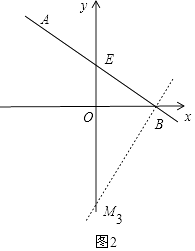
��3����ͼ2���Ե�AΪֱ�Ƕ�������CAD=90�㣬����AC��x��ĸ��������C������AD��y��ĸ��������D������CAD�Ƶ�A��תʱ��OC��OD��ֵ�Ƿ����仯�������䣬ֱ��д������ֵ�����仯��ֱ��д�����ı仯��Χ����Ҫ������̣���
���𰸡�
��1��
��ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0����
�ߵ�A����4��4������B��0��2����ֱ��AB�ϣ�
�� ![]() �����
����� 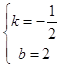 ��
��
��ֱ��AB�Ľ���ʽΪ��y=�� ![]() x+2
x+2
��2��
�ߡ�ABM����ABΪֱ�DZߵ�ֱ�������Σ�
���С�BAM=90����ABM=90�㣬
�ٵ���BAM=90��ʱ����ͼ1��
��A��AB�Ĵ��ߣ���x���ڵ�M1����y���ڵ�M2��
���֪��AEM1�ס�BEA��
�� ![]() =
= ![]() ��
��
�ɣ�1����֪OE=OB=AE=4��
�� ![]() =
= ![]() �����M1E=2��
�����M1E=2��
��OM1=2+4=6��
��M1����6��0����
��AE��y�ᣬ
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����OM2=12��
�����OM2=12��
��M2��0��12����
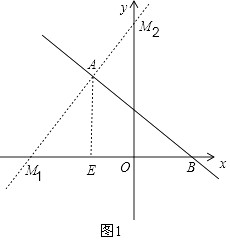
�ڵ���ABM=90��ʱ����ͼ2��
��B��AB�Ĵ��ߣ���y���ڵ�M3��
��ֱ��AB��y���ڵ�E�����ɣ�1����֪E��0��2����
��OE=2��OB=4��
�������֪��BOE�ס�M3OB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����OM3=8��
�����OM3=8��
��M3��0����8����
���Ͽ�֪��M������Ϊ����6��0����0��12����0����8��
��3��
���䣮
�������£�
����A�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪG��H����ͼ3��
���AGC=��AHD=90�㣬
�֡ߡ�HOC=90�㣬
���GAH=90�㣬
���DAG+��DAH=90�㣬
�ߡ�CAD=90�㣬
���DAG+��CAG=90�㣬
���CAG=��DAH��
��A����4��4����
��OG=AH=AG=OH=4��
�ڡ�AGC�͡�AHD��
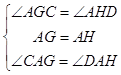
���AGC�ա�AHD��ASA����
��GC=HD��
��OC��OD=��OG+GC������HD��OH��=OG+OH=8��
��OC��OD��ֵ�������仯��ֵΪ8
����������1����A��B������������ô���ϵ���������ֱ��AB�Ľ���ʽ����2���ֱ��A��B������AB�Ĵ��ߣ���������Ľ��㼴Ϊ�����M�㣬�ٽ�����������ε��������OM�ij�������õ�M�����ꣻ��3����A�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪE��F����֤����AEC�ա�AFD���ɵõ�EC=FD���Ӷ��ɰ�OC��ODת��ΪFD��OD���������߶εĺͲ�����OC��OD=OE+OF=8��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2x��k=0����������ȵ�ʵ��������ʵ��k��ȡֵ��Χ�ǣ� ��
A.k��1
B.k��1
C.k�ݩ�1
D.k����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��һԪ���η���x2+x��2014��0������������a2+2a+b��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ��������룬������չ�о�������Ŀ���ɴﵽ��һ��֪һ���Ŀ�ģ�������һ���������벹��������
ԭ�⣺��ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬����EF���Բ���EF��BE��DF֮���������ϵ��
��1��˼·����
�ѡ�ABE�Ƶ�A��ʱ����ת90������ADG����ʹAB��AD�غϣ��ɡ�ADG=��B=90�㣬�á�FDG=180�㣬����F��D��G���ߣ���֤��AFG�� �� ��EF��BE��DF֮���������ϵ
Ϊ ��
��2���������
��ͼ2����E��F�ֱ���������ABCD�ı�CB��DC���ӳ����ϣ���EAF=45�㣬����EF���Բ���EF��BE��DF֮���������ϵΪ �� ������֤����
��3��������չ
��ͼ3���ڡ�ABC�У���BAC=90�㣬AB=AC����D��E���ڱ�BC�ϣ��ҡ�BAD+��EAC=45�㣬��BD=3��EC=6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����У����鷽ʽѡ����ȷ���ǣ� ��
A. Ϊ���˽�10000�����ݵ�ʹ��������ѡ��ȫ�����
B. Ϊ���˽�ij��ȫ����ο�������ѡ���������
C. Ϊ���˽�������50ö�ڵ���ɱ�˰뾶��ѡ��ȫ�����
D. Ϊ���˽�һ����װʳƷ�Ƿ��з�������ѡ��ȫ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������22 �� ����2��3 �� ��|��2|�� ![]() ����С�����˳������Ϊ�� ��
����С�����˳������Ϊ�� ��
A.����2��3����22����|��2|�� ![]()
B.![]() ����|��2|����22������2��3
����|��2|����22������2��3
C.��|��2|�� ![]() ����22������2��3
����22������2��3
D.��22������2��3�� ![]() ����|��2|
����|��2|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A1��A2��A3������x���ϣ���B1��B2��B3������ֱ��![]() �ϣ���OA1B1����B1A1A2����B2B1A2����B2A2A3����B3B2A3�����ǵ���ֱ�������Σ���OA1=1�����B2015�������ǣ� ��
�ϣ���OA1B1����B1A1A2����B2B1A2����B2A2A3����B3B2A3�����ǵ���ֱ�������Σ���OA1=1�����B2015�������ǣ� ��

A����![]() ��
��![]() �� B����
�� B����![]() ��
��![]() �� C����
�� C����![]() ��
��![]() �� D����
�� D����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
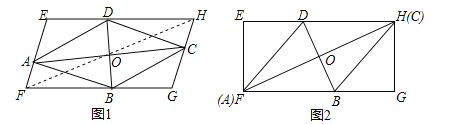
����Ŀ����ͼ��1��������ABCD�Խ���AC��BD�Ľ���O���ı���EFGH�Խ���FH���е㣬�ĸ�����A��B��C��D�ֱ����ı���EFGH�ı�EF��FG��GH��HE�ϣ�
��1����֤���ı���EFGH��ƽ���ı��Σ�
��2����ͼ��2�����ı���EFGH�Ǿ��Σ���AC��FH�غ�ʱ����֪![]() ��������ABCD�������20�������EFGH�ij������
��������ABCD�������20�������EFGH�ij������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com