
ΓΨΧβΡΩΓΩ »γΆΦ,RtΓςABC ÷–,ΓœACB=90 ,AC=6cm,BC=8cm,Ε·Βψ P ¥”Βψ B ≥ωΖΔ,‘Ύ BA±Ώ…œ“‘ΟΩΟκ 5cm ΒΡΥΌΕ»œρΒψ A ‘»ΥΌ‘ΥΕ·,Ά§ ±Ε·Βψ Q ¥”Βψ C ≥ωΖΔ,‘Ύ CB ±Ώ…œ“‘ΟΩΟκ 4cm ΒΡ ΥΌΕ»œρΒψ B ‘»ΥΌ‘ΥΕ·,‘ΥΕ· ±ΦδΈΣ t Οκ(0<t<2)Θ§Ν§Ϋ” PQ.
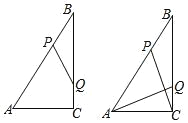
(1)»τΓςBPQ ”κΓςABC œύΥΤΘ§«σ t ΒΡ÷ΒΘΜ
(2)Β± t ΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–Έ ACQP ΒΡΟφΜΐΉν–ΓΘ§Ήν–Γ÷Β «Εύ…Ό?
(3)Ν§Ϋ” AQΘ§CPΘ§»τ AQΓΆCPΘ§«σ t ΒΡ÷ΒΓΘ
ΓΨ¥πΑΗΓΩ(1) ΘΚΒ± t=1 Μρ t=![]() ±Θ§ΓςBPQ ”κΓςABC œύΥΤ;(2)18;(3) t=
±Θ§ΓςBPQ ”κΓςABC œύΥΤ;(2)18;(3) t=![]()
ΓΨΫβΈωΓΩ
ΗυΨίΧβ“βΓςBPQΓΉΓςBAC œύΥΤ‘ΌΫαΚœΧβ“βΝ–±» ΫΫβ¥π¥ΥΈ Θ§œ»ΥΡ±Ώ–Έ ACQP ΒΡΟφΜΐ Ϋ”ΟΚ§tΒΡ±μ¥ο Ϋ±μ Ψ≥ωά¥Θ§‘Ό«σΤδΉν–Γ÷ΒΘΜΙΐΒψ P Ής PMΓΆBC ”ΎΒψ MΘ§…η AQ ”κ CP œύΫΜ”ΎΒψ NΘ§œ»÷ΛΟςΓςACQΓΉCMPΘ§‘Όάϊ”ΟΫα¬έ«σt÷Β.
(1)ΔΌΓςBPQΓΉΓςBAC œύΥΤ ±Θ§‘ρ![]()
ÿBP=5tȧQC=4tȧAC=6cmȧBC=8cmȧ
Γύ![]() Θ§ΫβΒΟΘΚt=1ΘΜ
Θ§ΫβΒΟΘΚt=1ΘΜ
ΔΎΓςBPQΓΉΓςBCA œύΥΤ ±Θ§
‘ρ![]() ,Φ¥
,Φ¥![]() Θ§ΫβΒΟΘΚt=
Θ§ΫβΒΟΘΚt=![]()
ΉέΚœ…œ ωΘΚΒ± t=1 Μρ t=![]() ±Θ§ΓςBPQ ”κΓςABC œύΥΤΘ§
±Θ§ΓςBPQ ”κΓςABC œύΥΤΘ§
(2)Ής PMΓΆBC ”ΎΒψ M.‘ρΓςBPMΓΉΓςBACΘ§
Γύ![]() ,Φ¥
,Φ¥![]() Θ§ΫβΒΟΘ§PM=3tΘ§
Θ§ΫβΒΟΘ§PM=3tΘ§
…ηΥΡ±Ώ–Έ ACQP ΒΡΟφΜΐΈΣ y,”…Χβ“βΒΟΘΚy=![]() ΓΝ6ΓΝ8
ΓΝ6ΓΝ8![]() (84t)ΓΝ3t=6(t1)2+18
(84t)ΓΝ3t=6(t1)2+18
ΓύΒ± t=1 ±Θ§ΟφΜΐΉν–ΓΈΣ 18.
(3)ΙΐΒψ P Ής PMΓΆBC ”ΎΒψ MΘ§…η AQ ”κ CP œύΫΜ”ΎΒψ NΘ§‘ρ”– PB=3tΘ§MC=84tΘ§
ΓΏΓœNAC+ΓœNCA=90 ,ΓœPCM+ΓœNCA=90 Θ§ΓύΓœNAC=ΓœPCMΘ§ ”÷ΓΏΓœACQ=ΓœCMP=90 Θ§ΓύΓςACQΓΉCMPΘ§
Γύ![]() ,Φ¥
,Φ¥![]() Θ§ΫβΒΟΘΚt=
Θ§ΫβΒΟΘΚt=![]()


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§–ΓΜΣΦτΝΥΝΫΧθΩμΈΣ1ΒΡ÷ΫΧθΘ§ΫΜ≤φΒΰΖ≈‘Ύ“ΜΤπΘ§«“ΥϋΟ«Ϋœ–ΓΒΡΫΜΫ«ΈΣ60ΓψΘ§‘ρΥϋΟ«÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣΘ®ΓΓΓΓΘ©

A. 3 B. 2 C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥφΉ≈»ΥΟ«ΜΖ±Θ“β ΕΒΡ≤ΜΕœ‘ω«ΩΘ§Έ“ –Φ“ΆΞΒγΕ·Ή‘––≥ΒΒΡ”Β”–ΝΩ÷πΡξ‘ωΦ”Θ°ΨίΆ≥ΦΤΘ§Ρ≥–Γ«χ2009ΡξΒΉ”Β”–Φ“ΆΞΒγΕ·Ή‘––≥Β125ΝΨΘ§2011ΡξΒΉΦ“ΆΞΒγΕ·Ή‘––≥ΒΒΡ”Β”–ΝΩ¥οΒΫ180ΝΨΘ°
Θ®1Θ©»τΗΟ–Γ«χ2009ΡξΒΉΒΫ2012ΡξΒΉΦ“ΆΞΒγΕ·Ή‘––≥””–ΝΩΒΡΡξΤΫΨυ‘ω≥Λ¬ œύΆ§Θ§‘ρΗΟ–Γ«χΒΫ2012ΡξΒΉΒγΕ·Ή‘––≥ΒΫΪ¥οΒΫΕύ…ΌΝΨΘΩ
Θ®2Θ©ΈΣΝΥΜΚΫβΆΘ≥ΒΟ§ΕήΘ§ΗΟ–Γ«χΨωΕ®ΆΕΉ 3Άρ‘Σ‘ΌΫ®»τΗ…ΗωΆΘ≥ΒΈΜΘ§Ψί≤βΥψΘ§Ϋ®‘λΖ―”ΟΖ÷±πΈΣ “ΡΎ≥ΒΈΜ1000‘Σ/ΗωΘ§¬ΕΧλ≥ΒΈΜ200‘Σ/ΗωΘ°ΩΦ¬«ΒΫ ΒΦ “ρΥΊΘ§ΦΤΜ°¬ΕΧλ≥ΒΈΜΒΡ ΐΝΩ≤Μ…Ό”Ύ “ΡΎ≥ΒΈΜΒΡ2±ΕΘ§ΒΪ≤Μ≥§Ιΐ “ΡΎ≥ΒΈΜΒΡ2.5±ΕΘ§‘ρΗΟ–Γ«χΉνΕύΩ…Ϋ®ΝΫ÷÷≥ΒΈΜΗςΕύ…ΌΗωΘΩ ‘–¥≥ωΥυ”–Ω…ΡήΒΡΖΫΑΗΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§C «AB―”≥ΛœΏ…œ“ΜΒψΘ§CD”κΓ―Oœύ«–”ΎΒψEΘ§ADΓΆCD”ΎΒψDΘ°
Θ®1Θ©«σ÷ΛΘΚAEΤΫΖ÷ΓœDACΘΜ
Θ®2Θ©»τAB=4Θ§ΓœABE=60ΓψΘ§«σ≥ωΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
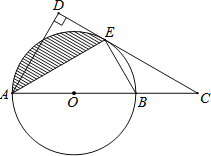
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «
«![]() ΒΡΗΏΘ§÷±œΏ
ΒΡΗΏΘ§÷±œΏ![]() Θ§
Θ§![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡΕ» ΐΈΣ______
ΒΡΕ» ΐΈΣ______![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2©¹2ax+cΘ®aΓΌ0Θ©”κy÷αΫΜ”ΎΒψCΘ®0Θ§4Θ©Θ§”κx÷αΫΜ”ΎΒψAΓΔBΘ§ΒψAΉχ±ξΈΣΘ®4Θ§0Θ©Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©≈ΉΈοœΏΒΡΕΞΒψΈΣNΘ§‘Ύx÷α…œ’““ΜΒψKΘ§ ΙCK+KNΉν–ΓΘ§≤Δ«σ≥ωΒψKΒΡΉχ±ξΘΜ
Θ®3Θ©ΒψQ «œΏΕΈAB…œΒΡΕ·ΒψΘ§ΙΐΒψQΉςQEΓΈACΘ§ΫΜBC”ΎΒψEΘ§Ν§Ϋ”CQΘ°Β±ΓςCQEΒΡΟφΜΐΉν¥σ ±Θ§«σΒψQΒΡΉχ±ξΘΜ
Θ®4Θ©»τΤΫ––”Ύx÷αΒΡΕ·÷±œΏl”κΗΟ≈ΉΈοœΏΫΜ”ΎΒψPΘ§”κ÷±œΏACΫΜ”ΎΒψFΘ§ΒψDΒΡΉχ±ξΈΣΘ®2Θ§0Θ©Θ°Έ ΘΚ «Ζώ¥φ‘Ύ’β―υΒΡ÷±œΏlΘ§ ΙΒΟΓςODF «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
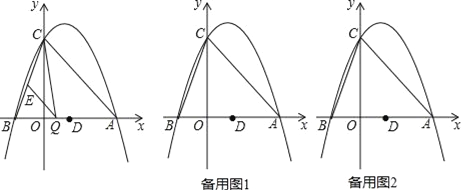
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΐ―ß…γΆ≈–ΓΉιœκάϊ”ΟΥυ―ßΒΡ÷Σ ΕΝΥΫβΡ≥ΙψΗφ≈ΤΒΡΗΏΕ»Θ®ΆΦ÷–GHΒΡ≥ΛΘ©Θ§Ψ≠≤βΝΩ÷ΣCD=2mΘ§‘ΎB¥Π≤βΒΟΒψDΒΡ―ωΫ«ΈΣ60ΓψΘ§‘ΎA¥Π≤βΒΟΒψCΒΡ―ωΫ«ΈΣ30ΓψΘ§AB=10mΘ§«“AΓΔBΓΔH»ΐΒψ‘Ύ“ΜΧθ÷±œΏ…œΘ§«κΗυΨί“‘…œ ΐΨίΦΤΥψGHΒΡ≥ΛΘ®![]() =1.73Θ§“Σ«σΫαΙϊΨΪ»ΖΒΟΒΫ0.1mΘ©
=1.73Θ§“Σ«σΫαΙϊΨΪ»ΖΒΟΒΫ0.1mΘ©
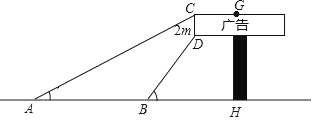
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐ![]() ΒΡ≤ΩΖ÷ΆΦœώ»γΆΦΥυ ΨΘ§ΆΦœώΙΐΒψ
ΒΡ≤ΩΖ÷ΆΦœώ»γΆΦΥυ ΨΘ§ΆΦœώΙΐΒψ![]() Θ§Ε‘≥Τ÷αΈΣ÷±œΏ
Θ§Ε‘≥Τ÷αΈΣ÷±œΏ![]() Θ§œ¬Ν–Ϋα¬έΘΚΘ®1Θ©
Θ§œ¬Ν–Ϋα¬έΘΚΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©»τΒψ
ΘΜΘ®3Θ©»τΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ‘ΎΗΟΚ· ΐΆΦœώ…œΘ§‘ρ
‘ΎΗΟΚ· ΐΆΦœώ…œΘ§‘ρ![]() ΘΜΘ®4Θ©»τΖΫ≥Χ
ΘΜΘ®4Θ©»τΖΫ≥Χ![]() ΒΡΝΫΗυΈΣ
ΒΡΝΫΗυΈΣ![]() ΚΆ
ΚΆ![]() Θ§«“
Θ§«“![]() Θ§‘ρ
Θ§‘ρ![]() Θ°Τδ÷–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «________.
Θ°Τδ÷–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2©¹2x+m©¹1=0”–ΝΫΗω Β ΐΗυx1Θ§x2Θ°
Θ®1Θ©«σmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©Β±x12+x22=6x1x2 ±Θ§«σmΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com