【题目】在
中，
，
，
是的高，直线，交于点
，则
的度数为______
.
【答案】
或
【解析】
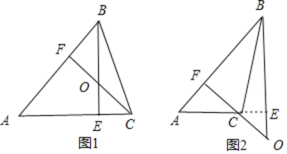
分两种情况讨论：如图1，点O在△ABC的内部，先利用四边形内角和得到∠EOF=180°-∠A=125°，则根据对顶角相等得到∠BOC的度数；如图2，点O在△ABC的外部，由于∠OCE=∠ACF，然后根据等角的余角相等可得到∠BOC=∠A=55°．
解：如图1，点O在△ABC的内部，
∵BE，CF是△ABC的高，
∴∠BEA=∠CFA=90°，
∴∠EOF=180°-∠A=180°-55°=125°，
∴∠BOC=125°；
如图2，点O在△ABC的外部，
∵BE，CF是△ABC的高，
∴∠BEA=∠CFA=90°，
∵∠OCE=∠ACF，
∴∠BOC=∠A=55°，
综上所述，∠BOC的度数为55°或125．
故答案为：55°或125．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1，在C1C2的延长线上取点C3，使D1C3＝D1C1，连接D1C3，以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2，在C2C3的延长线上取点C4，使D2C4＝D2C2，连接D2C4，以C3C4为边作等边△A3C3C4；…且点A1，A2，A3，…都在直线C1C2同侧，如此下去，可得到△A1C1C2，△A2C2C3，△A3C3C4，…，△AnCnCn＋1，则△AnCnCn＋1的周长为_______(n≥1，且n为整数)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角梯形纸片
中，
，
，
，将纸片沿过点
的直线折叠，使点
落在边
上的点
处，折痕为
．连接
并展开纸片．
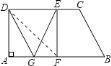
判断四边形
的形状，并说明理由．
取线段
的中点
，连接
、
，如果
，试说明四边形
是等腰梯形．
查看答案和解析>>
科目：初中数学 来源： 题型：
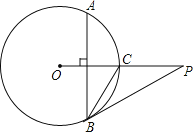
【题目】如图，已知P是⊙O外一点，PO交圆O于点C，OC=CP=2，弦AB⊥OC，劣弧AB的度数为120°，连接PB．
（1）求BC的长；
（2）求证：PB是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图,Rt△ABC 中,∠ACB=90 ,AC=6cm,BC=8cm,动点 P 从点 B 出发,在 BA边上以每秒 5cm 的速度向点 A 匀速运动,同时动点 Q 从点 C 出发,在 CB 边上以每秒 4cm 的 速度向点 B 匀速运动,运动时间为 t 秒(0<t<2)，连接 PQ.
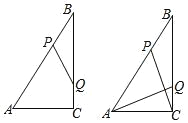
(1)若△BPQ 与△ABC 相似，求 t 的值；
(2)当 t 为何值时，四边形 ACQP 的面积最小，最小值是多少?
(3)连接 AQ，CP，若 AQ⊥CP，求 t 的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．
（1）求y与x的函数关系式；
（2）若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中，
，小聪同学利用直尺和圆规完成了如下操作：
①作
的平分线
交
于点
；
②作边
的垂直平分线
，与相交于点
；
③连接
，
.
请你观察图形解答下列问题：
（1）线段
，，之间的数量关系是________；
（2）若
，求
的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把抛物线y=
x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=x2交于点Q，则图中阴影部分的面积为 ▲ ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
