
分析 (1)由于长方形场地的宽为x米,根据周长为140米得出长为(70-x)米,再利用长方形场地的面积为1200平方米列出方程,解方程即可;
(2)由原来场地的长为(70-x)米,宽为x米,得出现在场地的长为(80-x)米,宽为(x-10)米,利用长方形的面积公式得出场地的面积减少值y=x(70-x)-(80-x)(x-10),化简整理得y=-20x+800,然后根据不等式的性质即可求解.
解答 解:(1)设宽为x米,则长为(70-x)米,由题意得
x(70-x)=1200,
解得x=30或40,
∵20≤x<35,
∴x=30;
(2)∵原来场地的长为(70-x)米,宽为x米,
∴现在场地的长为(80-x)米,宽为(x-10)米,
∴场地的面积减少了:x(70-x)-(80-x)(x-10)
=70x-x2-(80x-800-x2+10x)
=-20x+800,
∵20≤x<35,
∴100<-20x+800≤400,
即100<y≤400.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.也考查了不等式的性质.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | D. | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
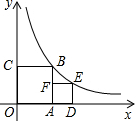 如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=$\frac{1}{x}$(x>0)的图象上,则:
如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=$\frac{1}{x}$(x>0)的图象上,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com