
【题目】如图,在Rt△ABC中,∠B=90°,BC=5 ![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 , AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(4)当t为何值,△BEF的面积是2 ![]() ?
?
【答案】
(1)10;5
(2)
解:EF与AD平行且相等.
证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
∴四边形AEFD为平行四边形.
∴EF与AD平行且相等
(3)
解:能;
理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又∵AE=DF,
∴四边形AEFD为平行四边形.
∵AB=BCtan30°=5 ![]() ×
× ![]() =5,
=5,
∴AC=2AB=10.
∴AD=AC﹣DC=10﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=10﹣2t,t= ![]() .
.
即当t= ![]() 时,四边形AEFD为菱形
时,四边形AEFD为菱形
(4)
解:∵在Rt△CDF中,∠A=30°,
∴DF= ![]() CD,
CD,
∴CF= ![]() t,
t,
又∵BE=AB﹣AE=5﹣t,BF=BC﹣CF=5 ![]() ﹣
﹣ ![]() t,
t,
∴ ![]() ,
,
即: ![]() ,
,
解得:t=3,t=7(不合题意舍去),
∴t=3.
故当t=3时,△BEF的面积为2 ![]() .
.
故答案为:5,10;平行且相等; ![]() ;3
;3
【解析】(1)解:∵在Rt△ABC中,∠C=30°,
∴AC=2AB,
根据勾股定理得:AC2﹣AB2=BC2 ,
∴3AB2=75,
∴AB=5,AC=10;
在Rt△ABC中,∠C=30°,则AC=2AB,根据勾股定理得到AC和AB的值.(2)先证四边形AEFD是平行四边形,从而证得AD∥EF,并且AD=EF,在运动过程中关系不变.(3)求得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件及求得.(4)BE=AB﹣AE=5﹣t,BF=BC﹣CF=5 ![]() ﹣
﹣ ![]() t,从而得到
t,从而得到 ![]() ,然后求得t的值.
,然后求得t的值.
【考点精析】掌握含30度角的直角三角形和勾股定理的概念是解答本题的根本,需要知道在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑,每台电子白板各多少万元?
(2)根据学校实际,需至少购进电脑和电子白板共30台,总费用不超过28万元,那么电子白板最多能买几台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.000 007 7 m,这个数用科学记数法表示为( )
A. 77×10-7B. 7.7×10-7C. 0.77×10-5D. 7.7×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,回答问题:
(1)在化简 ![]() 的过程中,小张和小李的化简结果不同;
的过程中,小张和小李的化简结果不同;
小张的化简如下: ![]() =
= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]()
小李的化简如下: ![]() =
= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]()
请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由.
(2)请你利用上面所学的方法化简 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截止2019年3月8日,中国科幻电影《流浪地球》的票房约为45.6亿元,成为中国科幻电影的里程碑.其中45.6亿用科学记数法表示为( )
A. 4.56×108B. 45.6×108C. 4.56×109D. 0.456×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( ) 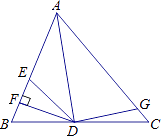
A.11
B.5.5
C.7
D.3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2017的坐标为( )
A.(504,﹣504)
B.(﹣504,504)
C.(﹣504,503)
D.(﹣505,504)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com