【题目】下列对矩形的判定：“
对角线相等的四边形是矩形；
对角线互相平分且相等的四边形是矩形；
有一个角是直角的四边形是矩形；
有四个角是直角的四边形是矩形；
四个角都相等的四边形是矩形；
对角线相等，且有一个直角的四边形是矩形；
一组邻边垂直，一组对边平行且相等的四边形是矩形；
对角线相等且互垂直的四边形是矩形”中，正确的个数有（ ）
A. 3个 B. 4个 C. 5个 D. 6个
【答案】B
【解析】
根据矩形的判定方法逐一进行判断即可得. 由矩形的判定方法得出（2）（4）（5）（7）正确，（1）（3）（6）（8）不正确，即可得出结论．
∵对角线相等的平行四边形是矩形，∴（1）不正确；
∵对角线互相平分且相等的四边形是矩形，∴（2）正确；（8）不正确；
∵有一个角是直角的平行四边形是矩形，∴（3）不正确；
∵有三个角是直角的四边形是矩形，∴（4）正确；
∵四边形的内角和等于360°，∴四个角都相等的四边是矩形，∴（5）正确；（6）不正确；
∵一组对边平行且相等的四边形是平行四边形，
∴一组邻边垂直，一组对边平行且相等的四边形是矩形，∴（7）正确；
正确的个数有4个，
故选B．
开心练习课课练与单元检测系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，BD是AC边上的高，延长BC至E，使CE=CD，连接DE。
（1）求∠E的度数？
（2）△DBE是什么三角形？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，平行四边形
的两条对角线相交于点
，
是
的中点，过点
作
的平行线，交
的延长线于点
，连结
．
求证：
；
当平行四边形满足什么条件时，四边形
是菱形？证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与
轴仅有一个公共点
，经过点的直线交该抛物线于点
，交
轴于点
，且点是线段
的中点．
求这条抛物线对应的函数解析式；
求直线对应的函数解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
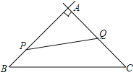
【题目】如图，在
中，
，
，
，现有动点
从点
出发，沿射线
方向运动，动点
从点
出发，沿射线
方向运动，已知点的速度是
，点的速度是
，它们同时出发，经过________秒，
的面积是面积的一半？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值
（1）（1+2x）（1﹣2x）﹣（x﹣3）2+5x（x﹣1），其中x＝﹣2
（2）[2（x﹣y）2﹣（2x+y）（x﹣2y）]÷4y，其中x＝﹣8，y＝1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个盒子中装有两个红色球，两个白色和一个蓝色球，这些球除颜色外都相同，从中随机摸出一个球，记下颜色后放回，再从中随机摸出一个球．
利用画树状图或列表的方法求摸到的两个球的颜色能配成紫色的概率（红色和蓝色可以配成紫色）；
若将题干中的“记下颜色后放回”改为“记下颜色后不放回”，请直接写出摸到的两个球的颜色能配成紫色的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
（
，
为常数）．
当
，
时，求二次函数的最小值；
当
时，若在函数值
的怙况下，只有一个自变量
的值与其对应，求此时二次函数的解析式；
当
时，若在自变量的值满足
的情况下，与其对应的函数值
的最小值为
，求此时二次函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一组有规律的图案，第1个图案由4个
组成，第2个图案由7个组成，第3个图案由10个组成，第4个图案由13个组成，…，君君有100个，她想按照这种规律组成一个最大的图案，则这个最大图案的一条边上的有____个．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com