
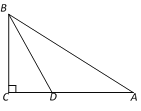
【题目】如图,在Rt△ABC中,∠ACB![]() 90°,∠ABC的平分线BD交AC于点D.
90°,∠ABC的平分线BD交AC于点D.
(1)求作⊙O,使得点O在边AB上,且⊙O经过B、D两点(要求尺规作图,保留作图痕迹,不写作法);
(2)证明AC与⊙O相切.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为_____,表示“D等级”的扇形的圆心角为_____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
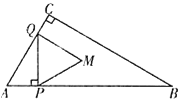
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以每秒2个单位的速度沿
出发以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() ,当点
,当点![]() 不和
不和![]() 的顶点重合时,以
的顶点重合时,以![]() 为边作等边三角形
为边作等边三角形![]() ,使点
,使点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,设点
的同侧,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)求等边三角形![]() 的边长(用含
的边长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边
的边![]() 上时,求
上时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)作直线![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,直接写出
,直接写出![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出门去遛狗(哈士奇,又名“撤手没”),当走到200米时狗绳突然断裂,脱了缰的哈士奇飞速跑开,小明也快速追狗,已知狗速是人速的2倍,4分钟时哈土奇听到小明的呼喊声,调头跑向小明,很快人狗相遇,但是哈士奇并没有停留的意思,继续跑向家中,小明调头继续追赶.脱缰之后狗和人的速度都不变.遛狗路程s(米)与时间t(分钟)之间的函数图象如图所示,下列说法:①a=500;②Y点纵坐标为580;③b=2;④c=7;⑤d=9;其中正确的个数是( )
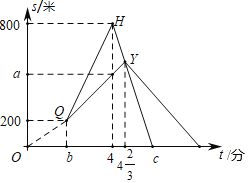
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
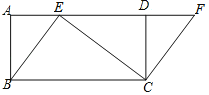
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与![]() 轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com