
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЙ§ЕуOЃЈ0ЃЌ0ЃЉЃЎAЃЈ8ЃЌ4ЃЉЃЌгыxжсНЛгкСэвЛЕуBЃЌЧвЖдГЦжсЪЧжБЯпxЃН3ЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєMЪЧOBЩЯЕФвЛЕуЃЌзїMNЁЮABНЛOAгкNЃЌЕБЁїANMУцЛ§зюДѓЪБЃЌЧѓMЕФзјБъЃЛ
ЃЈ3ЃЉPЪЧxжсЩЯЕФЕуЃЌЙ§PзїPQЁЭxжсгыХзЮяЯпНЛгкQЃЎЙ§AзїACЁЭxжсгкCЃЌЕБвдOЃЌPЃЌQЮЊЖЅЕуЕФШ§НЧаЮгывдOЃЌAЃЌCЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЪБЃЌЧѓPЕуЕФзјБъЃЎ
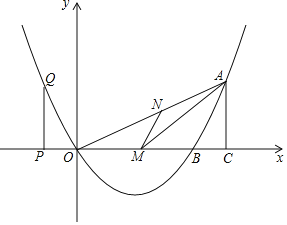
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕБtЃН3ЪБЃЌSЁїAMNгазюДѓжЕ3ЃЌДЫЪБMЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЛђЃЈЉ2ЃЌ0ЃЉЛђЃЈ4ЃЌ0ЃЉЛђЃЈ8ЃЌ0ЃЉЃЎ
ЃЛЃЈ2ЃЉЕБtЃН3ЪБЃЌSЁїAMNгазюДѓжЕ3ЃЌДЫЪБMЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЛђЃЈЉ2ЃЌ0ЃЉЛђЃЈ4ЃЌ0ЃЉЛђЃЈ8ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУХзЮяЯпЕФЖдГЦадШЗЖЈBЃЈ6ЃЌ0ЃЉЃЌШЛКѓЩшНЛЕуЪНЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЩшMЃЈtЃЌ0ЃЉЃЌЯШЦфЧѓГіжБЯпOAЕФНтЮіЪНЮЊ![]() жБЯпABЕФНтЮіЪНЮЊy=2x-12ЃЌжБЯпMNЕФНтЮіЪНЮЊy=2x-2tЃЌдйЭЈЙ§НтЗНГЬзщ
жБЯпABЕФНтЮіЪНЮЊy=2x-12ЃЌжБЯпMNЕФНтЮіЪНЮЊy=2x-2tЃЌдйЭЈЙ§НтЗНГЬзщ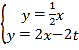 ЕУNЃЈ
ЕУNЃЈ![]() ЃЉЃЌНгзХРћгУШ§НЧаЮУцЛ§ЙЋЪНЃЌРћгУSЁїAMN=SЁїAOM-SЁїNOMЕУЕН
ЃЉЃЌНгзХРћгУШ§НЧаЮУцЛ§ЙЋЪНЃЌРћгУSЁїAMN=SЁїAOM-SЁїNOMЕУЕН![]() ШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
ШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЩшQ![]() ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЃЌЕБ
ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЃЌЕБ![]() ЪБЃЌЁїPQOЁзЁїCOAЃЌдђ
ЪБЃЌЁїPQOЁзЁїCOAЃЌдђ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌЁїPQOЁзЁїCAOЃЌдђ
ЪБЃЌЁїPQOЁзЁїCAOЃЌдђ![]() ЃЌШЛКѓЗжБ№НтЙигкmЕФОјЖджЕЗНГЬПЩЕУЕНЖдгІЕФPЕузјБъЃЎ
ЃЌШЛКѓЗжБ№НтЙигкmЕФОјЖджЕЗНГЬПЩЕУЕНЖдгІЕФPЕузјБъЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпЙ§дЕуЃЌЖдГЦжсЪЧжБЯпxЃН3ЃЌ
ЁрBЕузјБъЮЊЃЈ6ЃЌ0ЃЉЃЌ
ЩшХзЮяЯпНтЮіЪНЮЊyЃНaxЃЈxЉ6ЃЉЃЌ
АбAЃЈ8ЃЌ4ЃЉДњШыЕУa82ЃН4ЃЌНтЕУaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊyЃН![]() xЃЈxЉ6ЃЉЃЌМДyЃН
xЃЈxЉ6ЃЉЃЌМДyЃН![]() x2Љ
x2Љ![]() xЃЛ
xЃЛ
ЃЈ2ЃЉЩшMЃЈtЃЌ0ЃЉЃЌ
взЕУжБЯпOAЕФНтЮіЪНЮЊyЃН![]() xЃЌ
xЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊyЃНkx+bЃЌ
АбBЃЈ6ЃЌ0ЃЉЃЌAЃЈ8ЃЌ4ЃЉДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊyЃН2xЉ12ЃЌ
ЁпMNЁЮABЃЌ
ЁрЩшжБЯпMNЕФНтЮіЪНЮЊyЃН2x+nЃЌ
АбMЃЈtЃЌ0ЃЉДњШыЕУ2t+nЃН0ЃЌНтЕУnЃНЉ2tЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊyЃН2xЉ2tЃЌ
НтЗНГЬзщ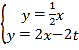 ЕУ
ЕУ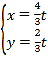 ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЁрSЁїAMNЃНSЁїAOMЉSЁїNOM
![]()
![]()
![]() ЃЌ
ЃЌ
ЕБtЃН3ЪБЃЌSЁїAMNгазюДѓжЕ3ЃЌДЫЪБMЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ
ЁпЁЯOPQЃНЁЯACOЃЌ
ЁрЕБ![]() ЪБЃЌЁїPQOЁзЁїCOAЃЌМД
ЪБЃЌЁїPQOЁзЁїCOAЃЌМД![]() ЃЌ
ЃЌ
ЁрPQЃН2POЃЌМД![]() ЃЌ
ЃЌ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН14ЃЌДЫЪБPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН14ЃЌДЫЪБPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЃЛ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃНЉ2ЃЌДЫЪБPЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃНЉ2ЃЌДЫЪБPЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЛ
ЁрЕБ![]() ЪБЃЌЁїPQOЁзЁїCAOЃЌМД
ЪБЃЌЁїPQOЁзЁїCAOЃЌМД![]() ЃЌ
ЃЌ
ЁрPQЃН![]() POЃЌМД
POЃЌМД![]() ЃЌ
ЃЌ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН8ЃЌДЫЪБPЕузјБъЮЊЃЈ8ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН8ЃЌДЫЪБPЕузјБъЮЊЃЈ8ЃЌ0ЃЉЃЛ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН4ЃЌДЫЪБPЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН4ЃЌДЫЪБPЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЛ
злЩЯЫљЪіЃЌPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЛђЃЈЉ2ЃЌ0ЃЉЛђЃЈ4ЃЌ0ЃЉЛђЃЈ8ЃЌ0ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДДаТаЁзщвЊВтСПЙЋдАФквЛПУЪїЕФИпЖШABЃЌЦфжавЛУћаЁзщГЩдБеОдкОрРыЪї10УзЕФЕуEДІЃЌВтЕУЪїЖЅAЕФбіНЧЮЊ54Ёу.вбжЊВтНЧвЧЕФМмИпCEЃН1.8УзЃЌдђетПХЪїЕФИпЖШЮЊ_________Уз.ЃЈНсЙћБЃСєвЛЮЛаЁЪ§.ВЮПМЪ§ОнЃКsin54ЁуЃН0.8090ЃЌcos54ЁуЃН0.5878ЃЌtan54ЁуЃН1.3764ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌЕуCЁЂЕуDЮЊЁбOЩЯвьгкAЁЂBЕФСНЕуЃЌСЌНгCDЃЌЙ§ЕуCзїCEЁЭDBЃЌНЛDBЕФбгГЄЯпгкЕуEЃЌСЌНгACЁЂADЁЂBCЃЌШєЁЯABD=2ЁЯBDCЃЎ
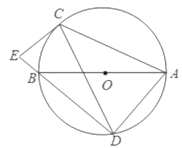
ЃЈ1ЃЉЧѓжЄЃКCEЪЧЁб0ЕФЧаЯп
ЃЈ2ЃЉЧѓжЄЃКЁїABC![]() ЁїCBE
ЁїCBE
ЃЈ3ЃЉШєЁбOЕФАыОЖЮЊ5ЃЌtanЁЯBDC=![]() ЃЌЧѓBEЕФГЄЃЎ
ЃЌЧѓBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
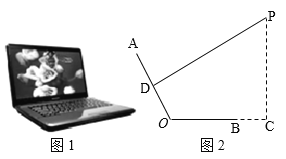
ЁОЬтФПЁПШчЭМ1ЪЧвЛЬЈЗХжУдкЫЎЦНзРУцЩЯЕФБЪМЧБОЕчФдЃЌНЋЦфВрУцГщЯѓГЩШчЭМ2ЫљЪОЕФМИКЮЭМаЮ.ШєЯдЪОЦСAOгыМќХЬBOГЄОљЮЊ24cmЃЌЕуPЮЊблОІЫљдкЮЛжУЃЌDЮЊAOЕФжаЕуЃЌСЌНгPDЃЌЧвPDЁЭAOЃЈДЫЪБЕуPЮЊзюМбЪгНЧЃЉЃЌЕуCдкOBЕФбгГЄЯпЩЯЃЌPCЁЭBCЃЌBCЃН12cm.
ЃЈ1ЃЉЕБPAЃН45cmЪБЃЌЧѓPCЕФГЄЃЛ
ЃЈ2ЃЉЕБЁЯAOCЃН115ЁуЪБЃЌЯпЖЮPCЕФГЄБШЃЈ1ЃЉжаЯпЖЮPCЕФГЄЪЧдіДѓЛЙЪЧМѕаЁЃПЧыЭЈЙ§МЦЫуЫЕУїЃЎЃЈНсЙћОЋШЗЕН0.1cmЃЌsin65ЁуЁж0.91ЃЌcos65ЁуЁж0.42ЃЌtan65ЁуЁж2.14ЃЌsin25ЁуЁж0.42ЃЌcos25ЁуЁж0.91ЃЌtan25ЁуЁж0.47ЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊгНгЪЎЖўдЫЃЌФГаЃПЊЩшСЫAЃКРКЧђЃЌBЃКыІЧђЃЌCЃКЬјЩўЃЌDЃКНЁУРВйЫФжжЬхг§ЛюЖЏЃЌЮЊСЫНтбЇЩњЖдетЫФжжЬхг§ЛюЖЏЕФЯВЛЖЧщПіЃЌдкШЋаЃЗЖЮЇФкЫцЛњГщШЁШєИЩУћбЇЩњЃЌНјааЮЪОэЕїВщЃЈУПИіБЛЕїВщЕФЭЌбЇБиаыбЁдёЖјЧвжЛФмдк4жаЬхг§ЛюЖЏжабЁдёвЛжжЃЉЃЎНЋЪ§ОнНјааећРэВЂЛцжЦГЩвдЯТСНЗљЭГМЦЭМЃЈЮДЛЭъећЃЉЃЎ

ЃЈ1ЃЉетДЮЕїВщжаЃЌвЛЙВВщСЫЁЁ ЁЁУћбЇЩњЃК
ЃЈ2ЃЉЧыВЙШЋСНЗљЭГМЦЭМЃК
ЃЈ3ЃЉШєга3УћзюЯВЛЖыІЧђдЫЖЏЕФбЇЩњЃЌ1УћзюЯВЛЖЬјЩўдЫЖЏЕФбЇЩњзщЖгЭтГіВЮМгвЛДЮСЊвъЛЅЛюЖЏЃЌгћДгжабЁГі2ШЫЕЃШЮзщГЄЃЈВЛЗже§ИБЃЉЃЌЧѓСНШЫОљЪЧзюЯВЛЖыІЧђдЫЖЏЕФбЇЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌКЏЪ§![]() гы
гы![]() ЕФЭМЯёдкЕквЛЯѓЯоФкНЛгкЕуAЃЌдкЧѓЕуAзјБъЪБЃЌаЁУїгЩгкПДДэСЫkЃЌНтЕУAЃЈ1 , 3ЃЉЃЛаЁЛЊгЩгкПДДэСЫmЃЌНтЕУAЃЈ1,
ЕФЭМЯёдкЕквЛЯѓЯоФкНЛгкЕуAЃЌдкЧѓЕуAзјБъЪБЃЌаЁУїгЩгкПДДэСЫkЃЌНтЕУAЃЈ1 , 3ЃЉЃЛаЁЛЊгЩгкПДДэСЫmЃЌНтЕУAЃЈ1, ![]() ЃЉЃЎ
ЃЉЃЎ
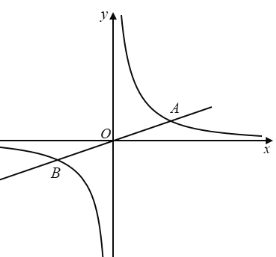
ЃЈ1ЃЉЧѓетСНИіКЏЪ§ЕФЙиЯЕЪНМАЕуAЕФзјБъЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓЛиД№ЃКШє![]() ЃЌЧыжБНгаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЃЌЧыжБНгаДГіxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊХзЮяЯп![]() ЃЎ
ЃЎ
(1)ЕБm=3ЪБЃЌЧѓХзЮяЯпЕФЖЅЕузјБъЃЛ
(2)вбжЊЕуA(1ЃЌ2)ЃЎЪдЫЕУїХзЮяЯпзмОЙ§ЕуAЃЛ
(3)вбжЊЕуB(0ЃЌ2)ЃЌНЋЕуBЯђгвЦНвЦ3ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуCЃЌШєХзЮяЯпгыЯпЖЮBCжЛгавЛИіЙЋЙВЕуЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
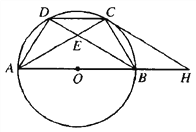
ЁОЬтФПЁПШчЭМЃЌЕуAЁЂBЁЂCЁЂDЪЧжБОЖЮЊABЕФЁбOЩЯЕФЫФИіЕуЃЌCDЃНBCЃЌACгыBDНЛгкЕуEЁЃ
ЃЈ1ЃЉЧѓжЄЃКDC2ЃНCEЁЄACЃЛ
ЃЈ2ЃЉШєAEЃН2ECЃЌЧѓ![]() жЎжЕЃЛ
жЎжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§ЕуCзїЁбOЕФЧаЯпЃЌНЛABЕФбгГЄЯпгкЕуHЃЌШєSЁїACHЃН![]() ЃЌЧѓECжЎГЄ.
ЃЌЧѓECжЎГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛИБРКМмгЩХфжиЁЂжЇМмЁЂРКАхгыРКП№зщГЩЃЌдкСЂжљЕФCЕуЙлВьРКАхЩЯбиDЕуЕФбіНЧЮЊ45ЁуЃЌдкжЇМмЕзЖЫЕФAЕуЙлВьРКАхЩЯбиDЕуЕФбіНЧЮЊ54ЁуЃЌЕуCгыРКАхЯТбиЕуEдкЭЌвЛЫЎЦНЯпЃЌШєAB=1.91УзЃЌРКАхИпЖШDEЮЊ1.05УзЃЌЧѓРКАхЯТбиEЕугыЕиУцЕФОрРыЃЎЃЈНсЙћОЋШЗЕН0ЃЎ1mЃЌВЮПМЪ§ОнЃКsin54ЁуЁж0.80ЃЌ cos54ЁуЁж0.60ЃЌtan54ЁуЁж1.33ЃЉ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com