
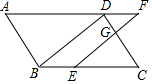
 如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.
如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.分析 (1)由四边形ABCD是平行四边形,得到AF∥BC,由于EF∥BD,推出四边形BDFE是平行四边形,根据平行四边形的性质即可得到结论;
(2)根据相似三角形的性质得到$\frac{DG}{GC}=\frac{DF}{EC}$,即$\frac{1}{2}$=$\frac{2}{EC}$,于是得到结论.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AF∥BC,
∵EF∥BD,
∴四边形BDFE是平行四边形,
∴BE=DF;
(2)∵BE=DF,BE=2,
∴DF=2,
∵AF∥BC,
∴△DGF∽△CGE,
∴$\frac{DG}{GC}=\frac{DF}{EC}$,即$\frac{1}{2}$=$\frac{2}{EC}$,
∴EC=4,
∴BC=BE+EC=2+4=6.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一面靠墙的空地上用长24m的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积S(m2).
如图,在一面靠墙的空地上用长24m的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积S(m2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知数轴上点A表示的数为-7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
如图,已知数轴上点A表示的数为-7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com