
����Ŀ���ۺ���ʵ��
�����龳��
��ѧ���ϣ���ʦ��ͬѧ�������Ŵ�С��ͬ��������ֽƬ����ת̽������������ѧ������Խ������ͼ��1�����ı���ABCD��DCGH���������Σ���M��N�ֱ���DH��CG���е㣬��������ABCD�Ե�DΪ���ģ���ʱ����ת�Ƕ�����0������90�������õ�������ABC'D��
������⣺
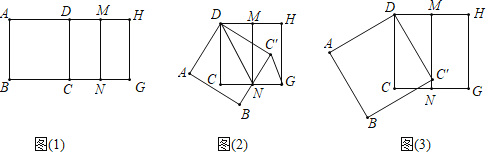
��������ȤС�����������ѧ���⣬��������Щ���⣮
��1����ͼ��2��������BC'���þ�����Nʱ��д���߶�C'G��DN��λ�ù�ϵ����֤��
��2����ͼ��3��������C����������MN��ʱ������ת�����Ĵ�С��
���𰸡���1��C��G��DN�����ɼ���������2����ת�����Ĵ�СΪ30�㣮
��������
��1�����ۣ�C��G��DN����취֤����DNC=��C��GN���ɽ�����⣮
��2������HC�䣮֤����DC��H�ǵȱ������μ��ɽ�����⣮
��1�����ۣ�C��G��DN��
���ɣ���ͼ2�У�����C��G��DN��
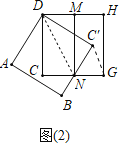
��Rt��DCN��Rt��DC��N��
��DC��DC����DN��DN����DCN����DC��N��90����
��Rt��DCN��Rt��DC��N��HL������
��CN��C��N����DNC����DNC����
����CN��NG��
��NG��C��N��
���NC��G����NGC����
���ߡ�CNC������NC��G+��NGC����
���DNC������NG C����
��C��G��DN��
��2������HC����
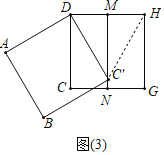
���ı���DCGH�������Σ���M��N�ֱ���DH��CG���е㣬
��MN��ֱƽ��DH��
��DC����C��H��
����DH��DC����
���DC��H�ǵȱ������Σ�
���C��DH��60����
���CDC����30����
����ת�����Ĵ�СΪ30����


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��С������7��) ��֪����ͼ��A�ǡ�O��һ�㣬�뾶OC���ӳ��������A��ֱ�߽���B�㣬OC=BC��AC=![]() OB��
OB��
��1����֤��AB�ǡ�O�����ߣ�
��2������ACD=45����OC=2������CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������Բ�����߷ֱ������ڵ�D��E��F�������е�ʽ��
�١�EDF����B��
��2��EDF����A����C��
��2��A����FED����EDF��
�ܡ�AED����BFE����CDF��180�������г����ĸ����ǣ�������
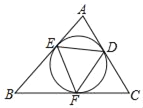
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼl�����ı���ABCD��.��DAB���Խ���ACƽ�֣���AC2=AB��AD�����dzƸ��ı���Ϊ���ɷ��ı��Ρ���DAB��Ϊ���ɷֽǡ�.

��1����ͼ2���ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ�����֤����DAC�ס�CAB.
��2����ͼ2���ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ��������DCB=��DAB ���DAB = .
��3�������ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ�����AC=4.BC=2.��D=90�㣬��AD= .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90������O��AB���е㣬��AC��6�����߳��㹻������ǰ��ֱ�Ƕ�����ڵ�O���������ǰ��Ƶ�0��ת��ʼ�ձ������ǰ��ֱ�DZ���AC�ཻ������Ϊ��E������ֱ�DZ���BC�ཻ������ΪD�������ֱ�����ǰ��ֱ�DZ߱����ǰ帲�Dz��ֵ������߶�CD��CE�ij���֮��Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����C��D����O�ϵĵ㣬��OC��BD��AD�ֱ���BC��OC����ڵ�E��F�������н��ۣ���AD��BD���ڡ�AOC=��AEC�� ��BCƽ����ABD���ܡ�CEF�ա�BED������һ����������_____��������Ϊ��ȷ���۵���Ŷ����ϣ���
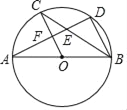
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ���abc��0����b��a+c����4a+2b+c��0����2c��3b����a+b��m ��am+b����m��1��ʵ������������ȷ���۵��У�������

A. �٢ڢ� B. �٢ۢ� C. �ۢܢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ���֪����x2+x��3=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
�⣺�����̵ĸ�Ϊy����y=2x������x=![]() ��
��
��x=![]() ������֪���̣��ã�
������֪���̣��ã�![]() ��2+
��2+![]() ��3=0������y2+2y��12=0��
��3=0������y2+2y��12=0��
������Ϊy2+2y��12=0��
�������÷��̸��Ĵ������·��̵ķ��������dz�Ϊ������������
���⣺��֪����x2+x��1=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���3����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() �ڵ�
�ڵ�![]()
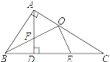
��1����![]() ʱ����
ʱ����![]() ��ֵ;
��ֵ;
��2����![]() ʱ��
ʱ��![]() ���ֵ;��
���ֵ;��![]() ��
��![]() ��Ҫд�������̣�
��Ҫд�������̣�
��3����![]() ʱ����
ʱ����![]() ��ֵ.��ֱ��д�������
��ֵ.��ֱ��д�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com