
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]()
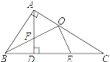
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 求的值;(
求的值;(![]() ,
,![]() 问要写出解答过程)
问要写出解答过程)
(3)当![]() 时,求
时,求![]() 的值.(直接写出结果)
的值.(直接写出结果)
【答案】(1)![]() =1;(2)
=1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() ,得到AC=2AB,又因为O为AC中点,推出AB=OC,利用AAS得出△ABF≌△COE,推出AF=CE,即可求出所求式子的比值;
,得到AC=2AB,又因为O为AC中点,推出AB=OC,利用AAS得出△ABF≌△COE,推出AF=CE,即可求出所求式子的比值;
(2)由![]() ,得到AB=AC,过A作AG平行于OE,交BC于点G,求出∠OEC=∠AGC,∠AFB=∠OEC,∠BAD=∠C=45°,利用AAS得出△AFB≌△CGA,推出AF=CG,得到E为CG的中点,即CE为CG的一半,即可求出所求式子的比.
,得到AB=AC,过A作AG平行于OE,交BC于点G,求出∠OEC=∠AGC,∠AFB=∠OEC,∠BAD=∠C=45°,利用AAS得出△AFB≌△CGA,推出AF=CG,得到E为CG的中点,即CE为CG的一半,即可求出所求式子的比.
(3)过A作AG平行于OE,交BC于点G,证△AFB∽△CGA,推出![]() ,再CG=2CE,代入求出即可.
,再CG=2CE,代入求出即可.
解:由![]() ,得到AC=2AB,
,得到AC=2AB,
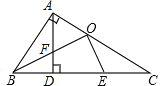
又∵O为AC的中点,
∴AC=2OC,
∴AB=OC,
又∵在Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD+∠ABC=90°,∠C+∠ABC=90°,
∴∠BAD=∠C,
又∵∠AFB=∠OBE+∠ADB,∠OEC=∠OBE+∠BOE,且∠ADB=∠BOE=90°,
∴∠AFB=∠OEC,
在△ABF和△COE中,
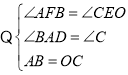
∴△ABF≌△COE(AAS),
∴AF=CE,
则![]() =1;
=1;
(2)过A作AG∥OE交BC于G,可得∠OEC=∠AGC,
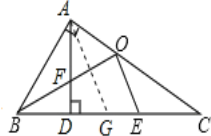
由(1)得∠AFB=∠OEC,
∴∠AFB=∠AGC,
又∵![]() ,即AB=AC,∠BAC=90°,AD⊥BC,
,即AB=AC,∠BAC=90°,AD⊥BC,
∴∠BAD=∠C=45°,
在△AFB和△CGA中,
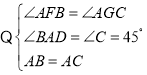
∴△AFB≌△CGA(AAS),
∴AF=CG,
![]()
![]()
![]()
(3)![]() ;
;
过A作AG平行于OE,交BC于点G,
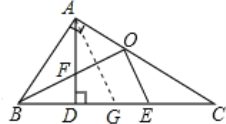
由(1)(2)可知∠BAD=∠C,∠AFB=∠CGA,
∴△AFB∽△CGA,
∵![]()
∴![]()
又∵CG=2CE,
∴![]()
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
数学课上,老师让同学们拿两张大小相同的正方形纸片做旋转探究活动,并提出数学问题加以解决:如图(1),四边形ABCD和DCGH都是正方形,点M,N分别是DH,CG的中点,将正方形ABCD以点D为中心,逆时针旋转角度α(0<α<90°),得到正方形ABC'D.
解决问题:
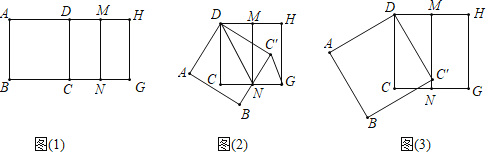
下面是兴趣小组提出两个数学问题,请你解决这些问题.
(1)如图(2).当边BC'正好经过点N时.写出线段C'G和DN的位置关系,并证明
(2)如图(3),当点C′正好落在MN上时,求旋转角α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车油箱的容积为![]() 升,小王把该车的油箱加满,从县城驾驶汽车到
升,小王把该车的油箱加满,从县城驾驶汽车到![]() 千米外的省城接客人,接到客人后立即按原路返回.请回答下列问题:
千米外的省城接客人,接到客人后立即按原路返回.请回答下列问题:
(1)油箱加满后,汽车能够行驶的总路程![]() (单位:千米)与平均耗油量
(单位:千米)与平均耗油量![]() (单位:升/千米)之间有怎样的函数关系?
(单位:升/千米)之间有怎样的函数关系?
(2)小王驾驶汽车去省城,平均每千米耗油![]() 升.返程时由于下雨,小王降低了车速,此时平均耗油量增加了一倍.小王不加油能否驾车回到县城?如果不能,至少还需加多少油才能保证回到县城?
升.返程时由于下雨,小王降低了车速,此时平均耗油量增加了一倍.小王不加油能否驾车回到县城?如果不能,至少还需加多少油才能保证回到县城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
(1)当k=3时,求函数图像与x轴的交点坐标;
(2)函数图像的对称轴与原点的距离为3,求k的值
(3)设二次函数图像上的一点P(x,y)满足![]() 时,y≤2,求k的取值范围。
时,y≤2,求k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABM=2∠BAM.
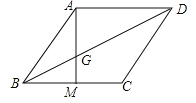
(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求三角形ADG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com