
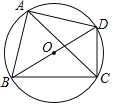
【题目】如图,BD是⊙O的直径,弦AC平分∠BCD,若四边形ABCD的面积为2,则AC=_____.
【答案】2
【解析】
设BC=a,CD=b,根据圆周角定理得到∠BAD=∠BCD=90°,根据勾股定理得到BD=![]() ,推出△ABD是等腰直角三角形,根据四边形的面积列方程得到a+b=2
,推出△ABD是等腰直角三角形,根据四边形的面积列方程得到a+b=2![]() (负值舍去),过B作BE⊥AC于E,过D作DF⊥AC于F,得到△CBE和△CDF是等腰直角三角形,求得BE=
(负值舍去),过B作BE⊥AC于E,过D作DF⊥AC于F,得到△CBE和△CDF是等腰直角三角形,求得BE=![]() BC=
BC=![]() a,DF=
a,DF=![]() CD=
CD=![]() b,于是得到结论.
b,于是得到结论.
解:设BC=a,CD=b,
∵BD是⊙O的直径,
∴∠BAD=∠BCD=90°,
∴BD=![]() ,
,
∵AC平分∠BCD,
∴![]() ,∠ACB=∠ACD=45°,
,∠ACB=∠ACD=45°,
∴AB=AD,
∴△ABD是等腰直角三角形,
∴四边形ABCD的面积=S△ABD+S△BCD=![]() (
(![]() )×
)×![]() (
(![]() )+
)+![]() ab=
ab=![]() (a2+b2)+
(a2+b2)+![]() ab=
ab=![]() (a+b)2=2,
(a+b)2=2,
∴a+b=![]() (负值舍去),
(负值舍去),
过B作BE⊥AC于E,过D作DF⊥AC于F,
则△CBE和△CDF是等腰直角三角形,
∴![]()
![]() ,
,![]()
![]() ,
,
∴四边形ABCD的面积=S△ABC+S△ACD=![]() ACBE+
ACBE+![]() ACDF=
ACDF=![]() (BE+CF)AC
(BE+CF)AC![]()
![]() ,
,
∴AC=2,
故答案为:2.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
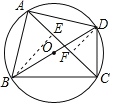
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
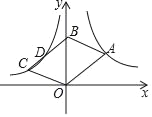
【题目】如图,直角坐标系中,A是反比例函数y=![]() (x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作ABCO.若点C及BC中点D都在反比例函数y=
(x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作ABCO.若点C及BC中点D都在反比例函数y=![]() (k<0,x<0)图象上,则k的值为( )
(k<0,x<0)图象上,则k的值为( )
A. ﹣3B. ﹣4C. ﹣6D. ﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
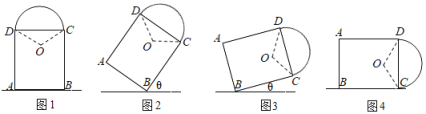
【题目】如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2![]() m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为___m.
m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为___m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
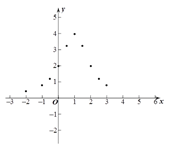
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】布袋中有红、黄、白三种乒乓球,个数依次为1个、2个、3个.除颜色外无其他差别,质感相同.
(1)小王随机地从袋中摸出1个乒乓球,摸出的是白色的概率是多少?
(2)小王随机地从袋中摸出两个乒乓球,求摸出的都是白色的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com