
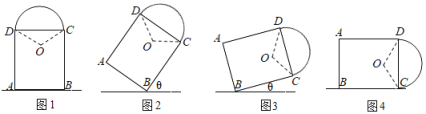
【题目】如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2![]() m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为___m.
m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为___m.
【答案】(2+2![]() ).
).
【解析】
利用勾股定理先求出圆弧的半径,然后分析出h取得最大值时为OB与地面垂直时,从而可解.
解:如图所示,过点O作垂直于地面的直线与拱门外框上沿交于点P,交地面于点Q,
如图1,AB,AD的长分别是2![]() m和4m,圆心角∠COD=120°,
m和4m,圆心角∠COD=120°,
∴∠DOP=60°,![]() DC=
DC=![]() AB=
AB=![]() ,
,
∴OD=2,PQ=5,
当点P在线段AD上时,拱门上的点到地面的最大距离h等于点D到地面的距离,即点P与点D重合时,此时
h=![]() ,
,
如图2所示,当点P在劣弧CD上时,拱门上的点到地面的最大距离h等于⊙O的半径长与圆心O到地面的距离之和,
易知,OQ≤OB,
而h=OP+OQ=2+OQ,
∴当点Q与点B重合时,h取得最大值,
由图1可知,OQ=3,BQ=![]() ,则OB=
,则OB=![]() ,
,
h的最大值为OP+OB,即2+![]() .
.
故答案为:(2+![]() ).
).


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与
的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() 。给出下列结论:①
。给出下列结论:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为
有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为![]() ,其中正确的结论有。其中正确的有_____________。(只需填写序号即可)
,其中正确的结论有。其中正确的有_____________。(只需填写序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
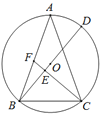
【题目】如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.
(1)求证:∠BFC=∠ABC.
(2)若⊙O的半径为5,CF=6,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,求作△ABC绕某点旋转一定角度后的△A′B′C′时,某同学只作了一部分图形.
(1)请把△A′B′C′作完整,并保留作图痕迹;
(2)写出基本作图步骤.
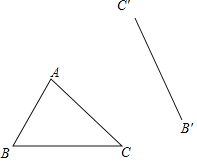
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
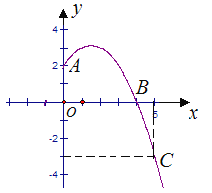
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com