
����Ŀ����ͼ���� Rt��POQ�У�OP=OQ=4��M �� PQ�е㣬��һ�����dz߶�����ڵ�M������MΪ��ת�ģ���ת���dzߣ����dzߵ���ֱ�DZ��� Rt��POQ����ֱ�DZ߷ֱ��ڵ�A��B��
��1����֤��MA=MB��
��2��̽��������ת���dzߵĹ����У��ı���AOBM������Ƿ����仯��Ϊʲô��
��3������ AB��̽��������ת���dzߵĹ����У���AOB���ܳ��Ƿ������Сֵ�������ڣ������Сֵ��
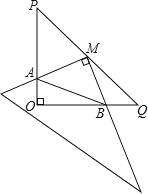
���𰸡���1������������2���ı��� AOBM �����û�з����仯�� ���ɼ���������3���� x=2 ʱ����AOB ���ܳ�����Сֵ����СֵΪ=4+2![]() ��
��
��������
��1������ M �� ME��OP �ڵ� E���� MF��OQ �ڵ� F�����������ε��ж������õ��ı��� OEMF �������Σ�֤����AME�ա�BMF������ȫ�������ε����ʽ��
��2������ȫ�������ε����ʵõ��ı��� AOBM �����=������ EOFM �������
��3������ȫ�������ε����ʵõ��õ� AE=BF���� OA=x�����ݹ��ɶ����õ�AB=![]() �����������ε��ܳ���ʽ�����κ��������ʽ��
�����������ε��ܳ���ʽ�����κ��������ʽ��
��1������ M �� ME��OP �ڵ� E���� MF��OQ �ڵ� F��
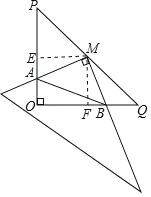
�ߡ�O=90�㣬��MEO=90�㣬��OFM=90�㣬
���ı��� OEMF �Ǿ��Σ�
��M �� PQ ���е㣬OP=OQ=4��
��ME=![]() OQ=2��MF=
OQ=2��MF=![]() OP=2��
OP=2��
��ME=MF��
���ı��� OEMF �������Σ�
�ߡ�AME+��AMF=90�㣬��BMF+��AMF=90�㣬
���AME=��BMF��
�ڡ�AME �͡�BMF �У�
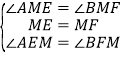
���AME�ա�BMF��ASA����
��MA=MB��
��2���ı��� AOBM �����û�з����仯�� �������£��ߡ�AME�ա�BMF��
���ı��� AOBM �����=������ EOFM �����=4��
��3���ߡ�AME�ա�BMF��
��AE=BF��
�� OA=x���� AE=2��x��
��OB=OF+BF=2+��2��x��=4��x��
�� Rt��AME ��AM=![]() =
= ![]() ��
��
�ߡ�AMB=90�㣬MA=MB��
��AB=![]() AM=
AM= ![]() ��
��
��AOB ���ܳ�=OA+OB+AB
=x+��4��x��+ ![]()
=4+![]() ��
��
�� x=2 ʱ����AOB ���ܳ�����Сֵ����СֵΪ=4+2![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����A����2��6��������x���ཻ�ڵ�B��������������y=3x��ͼ���ཻ�ڵ�C����C�ĺ�����Ϊ1��
��1����k��b��ֵ��
��2������D��y�Ḻ�����ϣ�������S��COD=![]() S��BOC�����D�����꣮
S��BOC�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
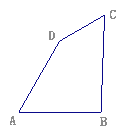
����Ŀ����֪����ͼ�����ı���ABCD�У�AB=AD=8����A=60������D=150��,�ı��ε��ܳ�Ϊ32����BC��DC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���֪��A��0��6������B��8��0��������P�ӵ�A��ʼ���߶�AO����ÿ��1����λ���ȵ��ٶ����O�ƶ���ͬʱ����Q�ӵ�B��ʼ���߶�BA����ÿ��2����λ���ȵ��ٶ����A�ƶ�,���P��Q�ƶ���ʱ��Ϊt�룮
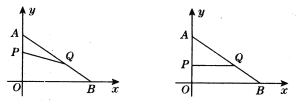
��1����ֱ��AB�Ľ���ʽ��
��2����tΪ��ֵʱ����APQ���AOB���ƣ�
��3����tΪ��ֵʱ����APQ�����Ϊ![]() ��ƽ����λ��
��ƽ����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90����D��BC���е㣬E��AD���е㣬����A��AF��BC��BE���ӳ����ڵ�F.
��1����֤����AEF�ա�DEB;
��2����֤���ı���ADCF������.
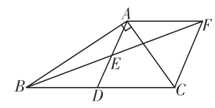
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��
��![]() ����˫����
����˫����![]() �ϣ�����˵���д�����ǣ� ��
�ϣ�����˵���д�����ǣ� ��
A.��![]() ����
����![]() B.��
B.��![]() ����
����![]()
C.��![]() ����
����![]() D.��
D.��![]() ����
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲���Уˮƽ������һ�ò����ʵ����ĸ߶ȣ�ѧУ��ѧ��ȤС����������̽�������ݹ�ķ��䶨�ɣ�����һ�澵�Ӻ�һ��Ƥ�ߣ��������ͼ��ʾ�IJ�����������һ���С�ľ���ˮƽ��������B�����ף�8.4�ĵ�E����Ȼ������ֱ��BE���˵���D����ʱǡ���ھ���������Ҷ���A������Ƥ������DE=3.2�ף��۲���Ŀ��CD=1.6�ף�����AB�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ��չ�����������ļ�ֵ�����ݽ���������ţ�1�����ţ�2������ݳ����ɼ���ѡ��5��ѡ�ֲμӸ������������ѡ����5��ѡ�ֵĸ����ɼ�������Ϊ100�֣���ͼ��ʾ������ͼ�����ݽ���������⣺
��1���ţ�1���ิ���ɼ�����λ������ ���֣��ţ�2���ิ���ɼ����������� ���֣�
��2��С��ͬѧ�Ѿ�����˾ţ�1���ิ����ƽ���ɼ�![]() =85�֣�����S2=
=85�֣�����S2=![]() [��85��85��2+��75��85��2+��80��85��2+��85��85��2+��100��85��2]=70����2������������ţ�2���ิ����ƽ���ɼ�x2�ͷ���S22��
[��85��85��2+��75��85��2+��80��85��2+��85��85��2+��100��85��2]=70����2������������ţ�2���ิ����ƽ���ɼ�x2�ͷ���S22��
��3�����ݣ�2���м������������ĸ��༶�ĸ����ɼ��Ϻã�
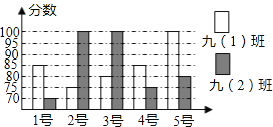
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ![]() ���������Ƶ�B��ʱ����ת30�㣬��ôͼ�е�M������Ϊ��������
���������Ƶ�B��ʱ����ת30�㣬��ôͼ�е�M������Ϊ��������
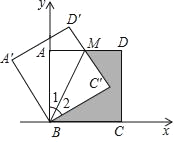
A.��![]() ��1��B.��1��
��1��B.��1��![]() ��C.��
��C.��![]() ��
��![]() ��D.��
��D.��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com