
分析 根据一次函数的增减性,可知本题分两种情况:①当k>0时,y随x的增大而增大,把x=-2,y=-6;x=5,y=-3代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式;②当k<0时,y随x的增大而减小,把x=-2,y=-3;x=5,y=-6代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式.
解答 解:分两种情况:
①当k>0时,把x=-2,y=-6;x=5,y=-3代入一次函数的解析式y=kx+b,
得$\left\{\begin{array}{l}{-2k+b=-6}\\{5k+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{7}}\\{b=-\frac{36}{7}}\end{array}\right.$.
则这个函数的解析式是y=$\frac{3}{7}$x-$\frac{36}{7}$;
②当k<0时,把x=-2,y=-3;x=5,y=-6代入一次函数的解析式y=kx+b,
得$\left\{\begin{array}{l}{-2k+b=-3}\\{5k+b=-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{7}}\\{b=-\frac{15}{7}}\end{array}\right.$.
则这个函数的解析式是y=-$\frac{3}{7}$x-$\frac{15}{7}$.
故这个函数的解析式是y=$\frac{3}{7}$x-$\frac{36}{7}$或y=-$\frac{3}{7}$x-$\frac{15}{7}$.
故答案为:y=$\frac{3}{7}$x-$\frac{36}{7}$或y=-$\frac{3}{7}$x-$\frac{15}{7}$.
点评 此题考查待定系数法求一次函数解析式,根据一次函数图象的性质分两种情况是解决本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
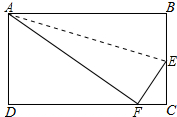 长方形纸片ABCD的长AB=10cm,宽BC=6cm,将它按如图方法折叠(以AE为折痕,点B落在CD边点F处),则△CEF的周长是8cm,面积是$\frac{8}{3}$cm2.
长方形纸片ABCD的长AB=10cm,宽BC=6cm,将它按如图方法折叠(以AE为折痕,点B落在CD边点F处),则△CEF的周长是8cm,面积是$\frac{8}{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
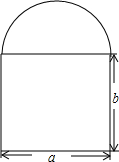 如图所示是某建筑物的窗户,上半部分为半圆形,下半部分为长方形,已知长方形的长,宽分别为a,b,这扇窗户的透光面积是$\frac{1}{8}$πa2+ab.
如图所示是某建筑物的窗户,上半部分为半圆形,下半部分为长方形,已知长方形的长,宽分别为a,b,这扇窗户的透光面积是$\frac{1}{8}$πa2+ab.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2y=5 | B. | 4x+6y=-6 | C. | 2x+4y=4 | D. | x+2y=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
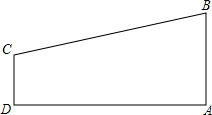 如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=3,CD=2,AD=7,在AD上是否存在点P,使△ABP与△DCP相似?如果存在,求出DP的值;如果不存在,试说明理由.
如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=3,CD=2,AD=7,在AD上是否存在点P,使△ABP与△DCP相似?如果存在,求出DP的值;如果不存在,试说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com