
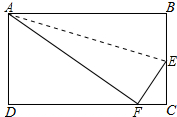
 长方形纸片ABCD的长AB=10cm,宽BC=6cm,将它按如图方法折叠(以AE为折痕,点B落在CD边点F处),则△CEF的周长是8cm,面积是$\frac{8}{3}$cm2.
长方形纸片ABCD的长AB=10cm,宽BC=6cm,将它按如图方法折叠(以AE为折痕,点B落在CD边点F处),则△CEF的周长是8cm,面积是$\frac{8}{3}$cm2. 分析 由翻折的性质可知AF=AB=10cm,BE=EF,依据勾股定理可知DF=8cm,从而得到FC=2cm,故此可知△CEF的周长=EF+EC+FC=BC+FC=8cm,设BE=EF=xcm,在△EFC中由勾股定理可求得x的值,从而可求得△EFC的面积.
解答 解:由翻折的性质可知:AF=AB=10cm,BE=EF.
在Rt△ADF中,DF=$\sqrt{A{F}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8cm.
∵FC=DC-DF,
∴FC=10-8=2cm.
∴三角形CEF的周长=EF+EC+FC=EB+EC+FC=6+2=8cm.
设EF=EB=xcm,则EC=(6-x)cm.
在Rt△EFC中,EF2=EC2+FC2,x2=(6-x)2+22.
解得:x=$\frac{10}{3}$.
∴EC=6-$\frac{10}{3}$=$\frac{8}{3}$.
∴△EFC的面积=$\frac{1}{2}×CF×CE$=$\frac{1}{2}×2×\frac{8}{3}$=$\frac{8}{3}$cm2.
故答案为:8cm;$\frac{8}{3}$cm2.
点评 本题主要考查的是翻折的性质、勾股定理的应用,根据勾股定理得到关于x的方程是解题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
| A. | |-a|是正数 | B. | -|a|是负数 | C. | $\sqrt{{a}^{2}}$是非负数 | D. | |-a|永远大于-|a| |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
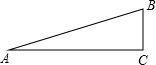 如图,在Rt△ABC中,∠C=90°,∠A=15°
如图,在Rt△ABC中,∠C=90°,∠A=15°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
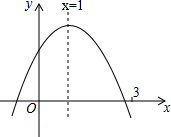 二次函数图象如图,下列结论:①abc<0;②2a-b=0;③对于任意实数m,都满足am2+bm≤a+b;④a-b+c>0;⑤若ax${\;}_{1}^{2}$+bx1=ax${\;}_{2}^{2}$+bx2,且x1≠x2,则x1+x2=2.其中正确的有①③⑤.(把正确的序号都填上)
二次函数图象如图,下列结论:①abc<0;②2a-b=0;③对于任意实数m,都满足am2+bm≤a+b;④a-b+c>0;⑤若ax${\;}_{1}^{2}$+bx1=ax${\;}_{2}^{2}$+bx2,且x1≠x2,则x1+x2=2.其中正确的有①③⑤.(把正确的序号都填上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com