
分析 (1)根据有理数的加法和减法进行计算即可;
(2)根据有理数的减法和乘法、除法进行计算即可;
(3)根据幂的乘方和有理数的乘法和减法进行计算即可;
(4)根据幂的乘方、有理数的乘法和除法进行计算即可.
解答 解:(1)(-20)+(+3)-(-5)-(+7)
=(-20)+3+5+(-7)
=-19;
(2)($\frac{2}{3}-\frac{1}{2}$)×30÷(-$\frac{1}{5}$)
=$\frac{1}{6}×30×(-5)$
=-25;
(3)23-$\frac{1}{14}×[2-(-3)^{2}]$
=8-$\frac{1}{14}×[2-9]$
=8-$\frac{1}{14}×(-7)$
=8+$\frac{1}{2}$
=8$\frac{1}{2}$;
(4)-22÷(-4)3+|0.8-1|×$(2\frac{1}{2})^{2}$
=-4×$\frac{1}{(-64)}$+0.2×$\frac{25}{4}$
=$\frac{1}{16}+\frac{5}{4}$
=$\frac{21}{16}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数加法减法,乘除法的计算方法.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
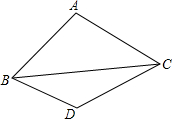 如图,在△ABC中,AB=AC,点D为△ABC外一点,且AC=CD,∠CBD=30°,求证:∠BDC=180°-$\frac{1}{2}$∠BAC.
如图,在△ABC中,AB=AC,点D为△ABC外一点,且AC=CD,∠CBD=30°,求证:∠BDC=180°-$\frac{1}{2}$∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-a|是正数 | B. | -|a|是负数 | C. | $\sqrt{{a}^{2}}$是非负数 | D. | |-a|永远大于-|a| |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com