
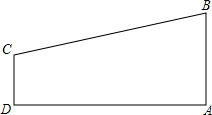
 如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=3,CD=2,AD=7,在AD上是否存在点P,使△ABP与△DCP相似?如果存在,求出DP的值;如果不存在,试说明理由.
如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=3,CD=2,AD=7,在AD上是否存在点P,使△ABP与△DCP相似?如果存在,求出DP的值;如果不存在,试说明理由. 分析 设DP=x,则AP=7-x,利用平行线的性质得∠D=∠A=90°,根据两组对应边的比相等且夹角对应相等的两个三角形相似,当$\frac{CD}{AB}$=$\frac{DP}{AP}$时,△DCP∽△ABP,即$\frac{2}{3}$=$\frac{x}{7-x}$;当$\frac{CD}{AP}$=$\frac{DP}{AB}$时,△DCP∽△APB,即$\frac{CD}{AP}$=$\frac{DP}{AB}$,即$\frac{2}{7-x}$=$\frac{x}{3}$,然后分别解方程求出x即可得到DP的长.
解答 解:存在.
设DP=x,则AP=7-x,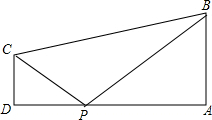
∵AB∥DC,
∴∠D=∠A=90°,
当$\frac{CD}{AB}$=$\frac{DP}{AP}$时,△DCP∽△ABP,即$\frac{2}{3}$=$\frac{x}{7-x}$,解得x=$\frac{14}{5}$;
当$\frac{CD}{AP}$=$\frac{DP}{AB}$时,△DCP∽△APB,即$\frac{CD}{AP}$=$\frac{DP}{AB}$,即$\frac{2}{7-x}$=$\frac{x}{3}$,整理得x2-7x+6=0,解得x1=1,x2=6.
综上所述,当DP为$\frac{14}{5}$或1或6时,△ABP与△DCP相似.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.运用分类讨论的思想是解决此题的关键.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
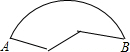 小明不慎把一个圆盘摔碎了,只剩下如图所示的一块比较完整的部分,他想找工人师傅做一个跟原来一样的圆盘,需要知道圆盘原来的形状,你能帮小明画出来吗?(用圆规、直尺作图,不写作法,但要保留作图痕迹.)
小明不慎把一个圆盘摔碎了,只剩下如图所示的一块比较完整的部分,他想找工人师傅做一个跟原来一样的圆盘,需要知道圆盘原来的形状,你能帮小明画出来吗?(用圆规、直尺作图,不写作法,但要保留作图痕迹.)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 与字母a,b都有关 | B. | 只与字母a有关 | C. | 只与字母b有关 | D. | 与字母a,b都无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com