
分析 根据题意画出图形,进而结合等腰三角形的性质结合锐角三角函数关系得出MC的长,再利用勾股定理得出答案.
解答 解:如图所示:
过点C作CF⊥AB于点F,延长ED交AB于点N,过点C作CM⊥ED于点M,
∵AB=4,
∴AF=BF=2,
∵tanB=2,
∴CF=4,
∴AC=BC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵D为AC边上的中点,
∴DC=$\sqrt{5}$,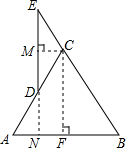
∵EC=$\sqrt{5}$,
∴△CED是等腰三角形,
∵AC=BC,CF⊥AB,
∴∠ACF=∠BCF,
∵EC=DC,
∴∠E=∠EDC,
∵∠E+∠EDC=∠ACF+∠BCF,
∴∠EDC=∠DCF,
∴ED∥FC,
∴∠ENF=90°,
可得四边形CMNF是矩形,
∵DN∥FC,AD=DC,
∴AN=NF=1,
∴MC=1,
∴EM=MD=2,
故DE=4.
点评 此题主要考查了解直角三角以及等腰三角形的性质和矩形的性质,正确得出MC的长是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
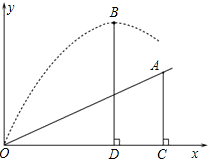 如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下
如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下查看答案和解析>>
科目:初中数学 来源: 题型:解答题
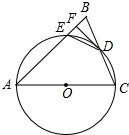 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com