
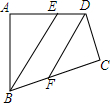
 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么? 科目:初中数学 来源: 题型:解答题
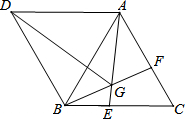 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 计算: (1)28+(-72) | (2)0+(-5) | (3)-$\frac{1}{5}$+(+$\frac{1}{6}$) |
| (4)(-3)-(-5) | (5)$({-3\frac{1}{2}})-5\frac{1}{4}$ | (6)(-8)+(-5)-(+5) |
| (7)-37-40+3-22 | (7)$(({-4})×({-\frac{3}{4}})×2$ | (8)(-5)×(-4)×3×(-2) |
| (9)-12÷$\frac{1}{4}÷({-\frac{8}{3}})$ | (10)$({\frac{1}{3}-\frac{5}{6}+\frac{7}{9}})÷({\frac{1}{18}})$ | (11)9$\frac{15}{16}×({-8})$ |
| (12)100÷$\frac{1}{8}×({-8})$ | (13)$1÷({-\frac{2}{7}})×\frac{1}{7}$ | (14)$\frac{1}{2}×({-\frac{4}{15}})÷\frac{2}{3}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
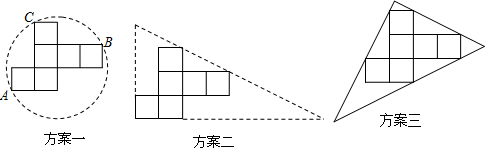
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com