
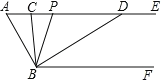
【题目】如图,已知AE∥BF,∠A=60°,点P为射线AE上任意一点(不与点A重合),BC,BD分别平分∠ABP和∠PBF,交射线AE于点C,点D.
(1)图中∠CBD= °;
(2)当∠ACB=∠ABD时,∠ABC= °;
(3)随点P位置的变化,图中∠APB与∠ADB之间的数量关系始终为 ,请说明理由.
【答案】(1)60 ;(2)30 ;(3)![]() ,见解析.
,见解析.
【解析】
(1)根据角平分线的定义只要证明∠CBD![]() ∠ABF即可;
∠ABF即可;
(2)想办法证明∠ABC=∠CBP=∠DBP=∠DBF即可解决问题;
(3)∠APB=2∠ADB.可以证明∠APB=∠PBF,∠ADB=∠DBF![]() ∠PBF.
∠PBF.
(1)∵AE∥BF,∴∠ABF=180°﹣∠A=120°.
又∵BC,BD分别平分∠ABP和∠PBF,∴∠CBD=∠CBP+∠DBP![]() (∠ABP+∠PBF)
(∠ABP+∠PBF)![]() ∠ABF=60°.
∠ABF=60°.
故答案为:60.
(2)∵AE∥BF,∴∠ACB=∠CBF.
又∵∠ACB=∠ABD,∴∠CBF=∠ABD,∴∠ABC=∠ABD﹣∠CBD=∠CBF﹣∠CBD=∠DBF,∴∠ABC=∠CBP=∠DBP=∠DBF,∴∠ABC![]() ∠ABF=30°.
∠ABF=30°.
故答案为:30.
(3)∠APB=2∠ADB.理由如下:
∵AE∥BF,∴∠APB=∠PBF,∠ADB=∠DBF.
又∵BD平分∠PBF,∴∠ADB=∠DBF![]() ∠PBF
∠PBF![]() ∠APB,即∠APB=2∠ADB.
∠APB,即∠APB=2∠ADB.



 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】下列抽样调查较为科学的是( )
![]() 为了解电饭锅的米饭是否熟了,小明从中任意取出一小匙米饭进行品尝
为了解电饭锅的米饭是否熟了,小明从中任意取出一小匙米饭进行品尝
![]() 为了解全区域市居民的生活水平,小华在区政府机关部分抽取了
为了解全区域市居民的生活水平,小华在区政府机关部分抽取了![]() 人做调查
人做调查
![]() 为了解某初级中学生的平均体重,小军在七至九年级各抽名学生进行调查
为了解某初级中学生的平均体重,小军在七至九年级各抽名学生进行调查
![]() 为了解重庆市2018年的平均气温,小琪上网查询了2018年12月份各天的气温情况
为了解重庆市2018年的平均气温,小琪上网查询了2018年12月份各天的气温情况
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
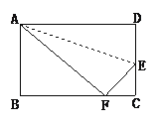
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).
(1)求BF的长;(2)求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC=8![]() ,BD=6
,BD=6![]() ,且
,且![]() ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )
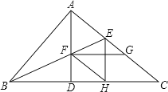
A.①②③④ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
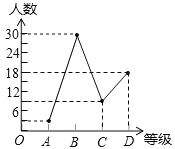
【题目】为迎接安顺市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
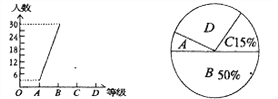
(2)补全折线统计图;
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________;
(4)若等级A为优秀,求该班的优秀率.
【答案】(1)60;(2)补图见解析;(3)108°;(4)5%.
【解析】(1)用B等人数除以其所占的百分比即可得到总人数;
(2)用求得的总人数乘以C等所占的百分比即可得到C等的人数,总人数减去A、C等的人数即可求得D等的人数;
(3)用D等的人数除以总人数乘以360°即可得到答案;
(4)用A等的人数除以总人数乘以100%即可得到答案. 解答:
解:(1)30÷50%=60(人)
∴八年级一共有60人。
(2)等级为“C”的人数为60×15%=9(人).
等级为“D”的人数为603309=18(人).
补全折线统计图如下。
(3)等极为“D”的部分所占圆心角的度数为![]() ×360°=108°,
×360°=108°,
故答案为:108°.
(4)该班的优秀率![]() ×100%=5%.
×100%=5%.
∴该班的优秀率为5%.
点睛:本题考查统计相关知识.利用拆线图与扇形图得出相关信息是解题的关键.
【题型】解答题
【结束】
25
【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴.
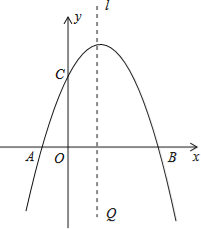
(1)求抛物线的函数关系式;
(2)求抛物线的顶点坐标;
(3)设P点是直线L上的一个动点,当△PAC的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
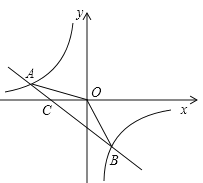
【题目】如图,已知A(-4,![]() )、B(2,-4)是一次函数
)、B(2,-4)是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与![]() 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积;
(3)求方程![]() 的解(直接写出答案)
的解(直接写出答案)
(4)求不等式![]() 的解集(直接写出答案)
的解集(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com