
ЎҫМвДҝЎҝДіРЈЙз»бКөјщРЎЧйОӘБЛІвБҝҙуСгЛюөДёЯ¶ИЈ¬ФЪөШГжЙПCҙҰҙ№ЦұУЪөШГжКъБўБЛёЯ¶ИОӘ2ГЧөДұкёЛCDЈ¬ҙЛКұөШГжЙПөДөгEЈ¬ұкёЛөД¶Ҙ¶ЛөгDЈ¬ҙуСгЛюөДЛюјвөгBХэәГФЪН¬Т»ЦұПЯЙПЈ¬ІаөГEC=4ГЧЈ¬Ҫ«ұкёЛCDПтәуТЖөҪөгGҙҰЈ¬ҙЛКұөШГжЙПөДөгFЈ¬ұкёЛөД¶Ҙ¶ЛөгHЈ¬ҙуСгЛюөДЛюјвөгBХэәГФЪН¬Т»ЦұПЯЙП(өгFЈ¬өгGЈ¬өгEЈ¬өгCУлЛюөЧҙҰөДөгAФЪН¬Т»ЦұПЯЙП)Ј¬ХвКұІвөГFG=6ГЧЈ¬GC=53ГЧЈ¬ЗлДгёщҫЭТФЙПКэҫЭЈ¬јЖЛгҙуСгЛюөДёЯ¶ИAB.
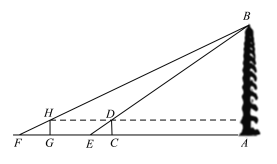
Ўҫҙр°ёЎҝҙуСгЛюөДёЯ¶ИABОӘ55ГЧ
ЎҫҪвОцЎҝ
УЙЎчEDCЎЧЎчEBAЈ¬ЎчFHGЎЧЎчFBAЈ¬ҝЙөГ![]() Ј¬
Ј¬![]() Ј¬ТтОӘDC=HGЈ¬НЖіц
Ј¬ТтОӘDC=HGЈ¬НЖіц![]() Ј¬БРіц·ҪіМЗуіцCA=106Ј¬УЙ
Ј¬БРіц·ҪіМЗуіцCA=106Ј¬УЙ![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬УЙҙЛјҙҝЙҪвҫцОКМвЈ®
Ј¬УЙҙЛјҙҝЙҪвҫцОКМвЈ®
ЎЯABЎНAFЈ¬CDЎНAFЈ¬HGЎНAFЈ¬
ЎаABЎОCDЎОHGЈ¬
ЎаЎчEDCЎЧЎчEBAЈ¬ЎчFHGЎЧЎчFBAЈ¬
Ўа![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ЎЯDC=HGЈ»
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаCA=106ГЧЈ¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаAB=55ГЧЈ¬
ҙрЈәҙуСгЛюөДёЯ¶ИABОӘ55ГЧЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,әҜКэ![]() әН
әН![]() (
(![]() КЗіЈКэ,ЗТ
КЗіЈКэ,ЗТ![]() )ФЪН¬Т»ЖҪГжЦұҪЗЧшұкПөөДНјПуҝЙДЬКЗЈЁ Ј©
)ФЪН¬Т»ЖҪГжЦұҪЗЧшұкПөөДНјПуҝЙДЬКЗЈЁ Ј©
A.  B.
B.  C.
C.  D.
D. 
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪТ»ҙОҫЫ»бЙПЈ¬№ж¶ЁГҝБҪёцИЛјыГжұШРлОХКЦЈ¬ЗТОХКЦ1ҙОЈ®
ЈЁ1Ј©ИфІОјУҫЫ»бөДИЛКэОӘ3Ј¬Фт№ІОХКЦЎЎ ЎЎҙОЈ»ИфІОјУҫЫ»бөДИЛКэОӘ5Ј¬Фт№ІОХКЦЎЎ ЎЎҙОЈ»
ЈЁ2Ј©ИфІОјУҫЫ»бөДИЛКэОӘnЈЁnОӘХэХыКэЈ©Ј¬Фт№ІОХКЦЎЎ ЎЎҙОЈ»
ЈЁ3Ј©ИфІОјУҫЫ»бөДИЛ№ІОХКЦ28ҙОЈ¬ЗлЗуіцІОјУҫЫ»бөДИЛКэЈ®
ЈЁ4Ј©јОјОУЙОХКЦОКМвПлөҪБЛТ»ёцКэС§ОКМвЈәИфПЯ¶ОABЙП№ІУРmёцөгЈЁІ»ә¬¶ЛөгAЈ¬BЈ©Ј¬ПЯ¶ОЧЬКэОӘ¶аЙЩДШЈҝЗлЦұҪУРҙіцҪбВЫЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИз№ы№ШУЪxөДТ»ФӘ¶юҙО·ҪіМax2+bx+cЈҪ0ЈЁaЎЩ0Ј©УРБҪёцКөКэёщЈ¬ЗТЖдЦРТ»ёцёщОӘБнТ»ёцёщөД2ұ¶Ј¬ДЗГҙіЖХвСщөД·ҪіМОӘЎ°ұ¶ёщ·ҪіМЎұЈ®АэИзЈ¬Т»ФӘ¶юҙО·ҪіМx2©Ғ6x+8ЈҪ0өДБҪёцёщКЗx1ЈҪ2әНx2ЈҪ4Ј¬Фт·ҪіМx2©Ғ6x+8ЈҪ0КЗЎ°ұ¶ёщ·ҪіМЎұЈ®
ЈЁ1Ј©ёщҫЭЙПКц¶ЁТеЈ¬Т»ФӘ¶юҙО·ҪіМ2x2+x©Ғ1ЈҪ0ЎЎ ЈЁМоЎ°КЗЎұ»тЎ°І»КЗЎұЈ©Ў°ұ¶ёщ·ҪіМЎұЈ®
ЈЁ2Ј©ИфТ»ФӘ¶юҙО·ҪіМx2©Ғ3x+cЈҪ0КЗЎ°ұ¶ёщ·ҪіМЎұЈ¬ФтcЈҪЎЎ Ј®
ЈЁ3Ј©Иф№ШУЪxөДТ»ФӘ¶юҙО·ҪіМax2+bx+cЈҪ0ЈЁaЎЩ0Ј©КЗЎ°ұ¶ёщ·ҪіМЎұЈ¬ФтaЎўbЎўcЦ®јдөД№ШПөОӘЎЎ Ј®
ЈЁ4Ј©ИфЈЁx©Ғ2Ј©ЈЁmx©ҒnЈ©ЈҪ0ЈЁmЎЩ0Ј©КЗЎ°ұ¶ёщ·ҪіМЎұЈ¬ЗуҙъКэКҪ4m2©Ғ5mn+n2өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
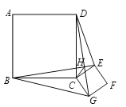
ЎҫМвДҝЎҝИзНјЈ¬Хэ·ҪРОABCDәНХэ·ҪРОCEFGөДұЯіӨ·ЦұрОӘaәНbЈ¬BEәНDGПаҪ»УЪөгHЈ¬Б¬ҪУHCЈ¬ёшіцПВБРҪбВЫЈәўЩBE=DGЈ»ўЪBEЎНDGЈ»ўЫDE2+BG2=2a2+2b2Ј¬ЖдЦРХэИ·өДҪбВЫКЗ__________.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ABКЗЎСOөДЦұҫ¶Ј¬өгCЎўDКЗФІЙПБҪөгЈ¬ЗТODЎОACЈ¬ODУлBCҪ»УЪөгE.

ЈЁ1Ј©ЗуЦӨЈәEОӘBCөДЦРөгЈ»
ЈЁ2Ј©ИфBCЈҪ8Ј¬DEЈҪ3Ј¬ЗуABөДіӨ¶ИЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ТСЦӘөг![]() Ј¬ТФФӯөгOОӘФІРДЎў3ОӘ°лҫ¶ЧчЎСOЈ¬ЎСOУлxЦбҪ»УЪөгBЎўC.өгPҙУөгOіц·ўЈ¬ТФГҝГл1ёцөҘО»өДЛЩ¶ИСШyЦбХэ°лЦбФЛ¶ҜЈ¬ФЛ¶ҜКұјдОӘ
Ј¬ТФФӯөгOОӘФІРДЎў3ОӘ°лҫ¶ЧчЎСOЈ¬ЎСOУлxЦбҪ»УЪөгBЎўC.өгPҙУөгOіц·ўЈ¬ТФГҝГл1ёцөҘО»өДЛЩ¶ИСШyЦбХэ°лЦбФЛ¶ҜЈ¬ФЛ¶ҜКұјдОӘ![]() .Б¬ҪбAPЈ¬Ҫ«
.Б¬ҪбAPЈ¬Ҫ«![]() СШAP·ӯХЫЈ¬өГөҪ
СШAP·ӯХЫЈ¬өГөҪ![]() Ј¬Зу
Ј¬Зу![]() УРТ»ұЯЛщФЪЦұПЯУлЎСOПаЗРКұ
УРТ»ұЯЛщФЪЦұПЯУлЎСOПаЗРКұ![]() өДЦө.
өДЦө.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪҫШРО![]() ЦРЈ¬Б¬Ҫб
ЦРЈ¬Б¬Ҫб![]() Ј¬өг
Ј¬өг![]() ҙУөг
ҙУөг![]() іц·ўЈ¬ТФГҝГл1ёцөҘО»өДЛЩ¶ИСШЧЕ
іц·ўЈ¬ТФГҝГл1ёцөҘО»өДЛЩ¶ИСШЧЕ![]() өДВ·ҫ¶ФЛ¶ҜЈ¬ФЛ¶ҜКұјдОӘ
өДВ·ҫ¶ФЛ¶ҜЈ¬ФЛ¶ҜКұјдОӘ![]() ЈЁГлЈ©. №эөг
ЈЁГлЈ©. №эөг![]() Чч
Чч![]() УЪөг
УЪөг![]() Ј¬ФЪҫШРО
Ј¬ФЪҫШРО![]() өДДЪІҝЧчХэ·ҪРО
өДДЪІҝЧчХэ·ҪРО![]() . ЈЁ
. ЈЁ![]() ФЪ
ФЪ![]() өДУТІаЈ©
өДУТІаЈ©

ЈЁ1Ј©ИзНјЈ¬өұ![]() КұЈ¬
КұЈ¬
ўЩИфөг![]() ФЪ
ФЪ![]() өДДЪІҝЈ¬Б¬Ҫб
өДДЪІҝЈ¬Б¬Ҫб![]() Ўў
Ўў![]() Ј¬ЗуЦӨЈә
Ј¬ЗуЦӨЈә![]() Ј»
Ј»
ўЪөұ![]() КұЈ¬ЙиХэ·ҪРО
КұЈ¬ЙиХэ·ҪРО![]() Ул
Ул![]() өДЦШөюІҝ·ЦГж»эОӘ
өДЦШөюІҝ·ЦГж»эОӘ![]() Ј¬Зу
Ј¬Зу![]() Ул
Ул![]() өДәҜКэ№ШПөКҪЈ»
өДәҜКэ№ШПөКҪЈ»
ЈЁ2Ј©өұ![]() КұЈ¬ИфЦұПЯ
КұЈ¬ИфЦұПЯ![]() Ҫ«ҫШРО
Ҫ«ҫШРО![]() өДГж»э·ЦіЙ
өДГж»э·ЦіЙ![]() БҪІҝ·ЦЈ¬Зу
БҪІҝ·ЦЈ¬Зу![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Хэ·ҪРОABCDөДұЯіӨКЗ3Ј¬BP=CQЈ¬Б¬ҪУAQЈ¬DPҪ»УЪөгOЈ¬Іў·ЦұрУлұЯCDЈ¬BCҪ»УЪөгFЈ¬EЈ¬Б¬ҪУAEЈ¬ПВБРҪбВЫЈәўЩAQЎНDPЈ»ўЪOA2=OEOPЈ»ўЫSЎчAOD=SЛДұЯРОOECFЈ»ўЬөұBP=1КұЈ¬tanЎПOAE=![]() Ј¬ЖдЦРХэИ·ҪбВЫөДёцКэКЗЈЁЎЎЎЎЈ©
Ј¬ЖдЦРХэИ·ҪбВЫөДёцКэКЗЈЁЎЎЎЎЈ©
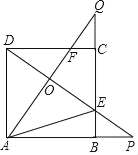
A. 1 B. 2 C. 3 D. 4
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com