
【题目】在矩形![]() 中,连结
中,连结![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着![]() 的路径运动,运动时间为
的路径运动,运动时间为![]() (秒). 过点
(秒). 过点![]() 作
作![]() 于点
于点![]() ,在矩形
,在矩形![]() 的内部作正方形
的内部作正方形![]() . (
. (![]() 在
在![]() 的右侧)
的右侧)

(1)如图,当![]() 时,
时,
①若点![]() 在
在![]() 的内部,连结
的内部,连结![]() 、
、![]() ,求证:
,求证:![]() ;
;
②当![]() 时,设正方形
时,设正方形![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若直线
时,若直线![]() 将矩形
将矩形![]() 的面积分成
的面积分成![]() 两部分,求
两部分,求![]() 的值.
的值.
【答案】(1)①见解析;②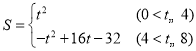 ;(2)
;(2)![]() 或
或![]() 或
或![]()
【解析】
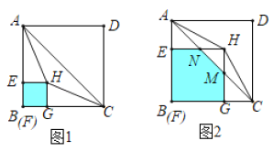
(1)①如图1中,证明△AEH≌△CGH(SAS)即可解决问题.
②分两种情形分别求解:如图1中,当0<t≤4时,重叠部分是正方形EFGH.如图2中,当4<t≤8时,重叠部分是五边形EFGMN.
(2)分三种情形分别求解:①如图31中,延长AH交BC于M,当BM=CM=4时,直线AH将矩形ABCD的面积分成1:3两部分.②如图32中,延长AH交CD于M交BC的延长线于K,当CM=DM=3时,直线AH将矩形ABCD的面积分成1:3两部分.③如图33中,当点E在线段AC上时,延长AH交CD于M,交BC的延长线于N.当CM=DM时,直线AH将矩形ABCD的面积分成1:3两部分.
(1)①如图1中,
∵四边形![]() 是正方形,
是正方形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②如图1中,当![]() 时,重叠部分是正方形
时,重叠部分是正方形![]() ,
,![]() .
.
如图2中,当![]() 时,重叠部分是五边形
时,重叠部分是五边形![]() ,
,
![]() .
.
综上所述,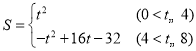 .
.
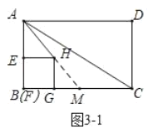
(2)如图3-1中,延长![]() 交
交![]() 于
于![]() ,
,
当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成
的面积分成![]() 两部分.
两部分.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
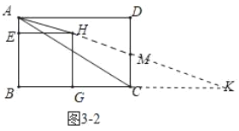
如图3-2 中,延长![]() 交
交![]() 于
于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,
当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成
的面积分成![]() 两部分,易证
两部分,易证![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
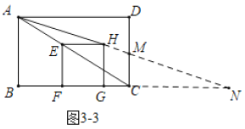
如图3-3 中,当点![]() 在线段
在线段![]() 上时,延长
上时,延长![]() 交
交![]() 于
于![]() ,交
,交![]() 的延长线于
的延长线于![]() .
.
当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成
的面积分成![]() 两部分,易证
两部分,易证![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴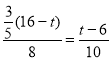 ,
,
解得![]() .
.
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在一个口袋里装着白、红、黑三种颜色的小球(除颜色外形状大小完全相同),其中白球3个、红球2个、黑球1个.
(1)随机从袋中取出一个球,求取出的球是黑球的概率;
(2)若取出的第一只球是红球,不将它放回袋里,从袋中余下的球中再随机地取出1个,这时取出的球是黑球的概率是多少?
(3)若取出一个球,将它放回袋中,从袋中再随机地取出一个球,两次取出的球都是白球的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,此时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,侧得EC=4米,将标杆CD向后移到点G处,此时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.
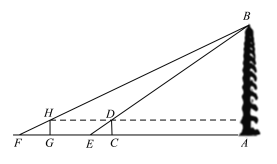
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
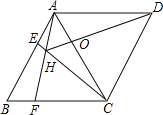
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排查和处置,在疫情排查过程中,某农场第一天发现3头生猪发病,两天后发现共有192头生猪发病,
(1)求每头发病生猪平均每天传染多少头生猪?
(2)若疫情得不到有效控制,3天后生猪发病头数会超过1500头吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )

A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
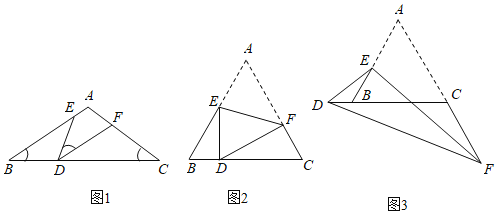
【题目】(1)模型探究:如图1,D、E、F分别为△ABC三边BC、AB、AC上的点,且∠B=∠C=∠EDF=a.△BDE与△CFD相似吗?请说明理由;
(2)模型应用:△ABC为等边三角形,其边长为8,E为AB边上一点,F为射线AC上一点,将△AEF沿EF翻折,使A点落在射线CB上的点D处,且BD=2.
①如图2,当点D在线段BC上时,求![]() 的值;
的值;
②如图3,当点D落在线段CB的延长线上时,求△BDE与△CFD的周长之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com