
ЁОЬтФПЁПШчЙћЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+cЃН0ЃЈaЁй0ЃЉгаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИіИљЮЊСэвЛИіИљЕФ2БЖЃЌФЧУДГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЎР§ШчЃЌвЛдЊЖўДЮЗНГЬx2Љ6x+8ЃН0ЕФСНИіИљЪЧx1ЃН2КЭx2ЃН4ЃЌдђЗНГЬx2Љ6x+8ЃН0ЪЧЁАБЖИљЗНГЬЁБЃЎ
ЃЈ1ЃЉИљОнЩЯЪіЖЈвхЃЌвЛдЊЖўДЮЗНГЬ2x2+xЉ1ЃН0ЁЁ ЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉЁАБЖИљЗНГЬЁБЃЎ
ЃЈ2ЃЉШєвЛдЊЖўДЮЗНГЬx2Љ3x+cЃН0ЪЧЁАБЖИљЗНГЬЁБЃЌдђcЃНЁЁ ЃЎ
ЃЈ3ЃЉШєЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+cЃН0ЃЈaЁй0ЃЉЪЧЁАБЖИљЗНГЬЁБЃЌдђaЁЂbЁЂcжЎМфЕФЙиЯЕЮЊЁЁ ЃЎ
ЃЈ4ЃЉШєЃЈxЉ2ЃЉЃЈmxЉnЃЉЃН0ЃЈmЁй0ЃЉЪЧЁАБЖИљЗНГЬЁБЃЌЧѓДњЪ§ЪН4m2Љ5mn+n2ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉВЛЪЧ ЃЛЃЈ2ЃЉ2ЃЛЃЈ3ЃЉ2b2ЃН9acЃЛЃЈ4ЃЉ0ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАБЖИљЗНГЬЁБЕФЖЈвхМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉИљОнБЖИљЗНГЬЕФЖЈвхвдМАИљгыЯЕЪ§ЕФЙиЯЕМДПЩЧѓГіД№АИЃЛ
ЃЈ3ЃЉЩшx=mгыx=2mЪЧЗНГЬax2+bx+c=0ЕФНтЃЌШЛКѓИљОнИљгыЯЕЪ§ЕФЙиЯЕМДПЩЧѓГіД№АИЃЛ
ЃЈ4ЃЉИљОнЖЈвхПЩЧѓГіn=4mЛђn=mЃЌДњШыдЪНКѓМДПЩЧѓГіД№АИЃЎ
НтЃКЃЈ1ЃЉ2x2+xЉ1ЃН0ЃЌ
ЃЈ2xЉ1ЃЉЃЈx+1ЃЉЃН0ЃЌ
НтЕУx1ЃН![]() КЭx2ЃНЉ1ЃЌ
КЭx2ЃНЉ1ЃЌ
ЙЪвЛдЊЖўДЮЗНГЬ2x2+xЉ1ЃН0 ВЛЪЧЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉЁАБЖИљЗНГЬЁБЃЛ
ЃЈ2ЃЉгЩЬтвтПЩжЊЃКxЃНmгыxЃН2mЪЧЗНГЬx2Љ3x+cЃН0ЕФНтЃЌ
Ёр2m+m=3ЃЌ2m2=cЃЌ
ЁрmЃН1ЃЌcЃН2ЃЛ
ЃЈ3ЃЉЩшxЃНmгыxЃН2mЪЧЗНГЬax2+bx+cЃН0ЕФНтЃЌ
Ёр2m+m=![]() ЃЌ2m2=
ЃЌ2m2=![]() ЃЌ
ЃЌ
ЁрЯћШЅmЕУЃК2b2ЃН9acЃЛ
ЃЈ4ЃЉгЩЃЈxЉ2ЃЉЃЈmxЉnЃЉЃН0ЃЈmЁй0ЃЉЪЧЁАБЖИљЗНГЬЁБЃЌ
ЧвИУЗНГЬЕФСНИљЗжБ№ЮЊxЃН2КЭxЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН4Лђ
ЃН4Лђ![]() ЃН1ЃЌМДnЃН4mЛђnЃНmЃЌ
ЃН1ЃЌМДnЃН4mЛђnЃНmЃЌ
ЕБnЃН4mЪБЃЌ
дЪНЃНЃЈmЉnЃЉЃЈ4mЉnЃЉЃН0
ЕБnЃНmЪБЃЌ
дЪНЃНЃЈmЉnЃЉЃЈ4mЉnЃЉЃН0ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
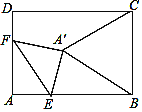
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=8ЃЌAD=6ЃЌЕуEЮЊABЩЯвЛЕуЃЌAE=2![]() ЃЌЕуFдкADЩЯЃЌНЋЁїAEFбиEFелЕўЃЌЕБелЕўКѓЕуAЕФЖдгІЕуAЁфЧЁКУТфдкBCЕФДЙжБЦНЗжЯпЩЯЪБЃЌелКлEFЕФГЄЮЊ_____ЃЎ
ЃЌЕуFдкADЩЯЃЌНЋЁїAEFбиEFелЕўЃЌЕБелЕўКѓЕуAЕФЖдгІЕуAЁфЧЁКУТфдкBCЕФДЙжБЦНЗжЯпЩЯЪБЃЌелКлEFЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіПкДќРязАзХАзЁЂКьЁЂКкШ§жжбеЩЋЕФаЁЧђЃЈГ§беЩЋЭтаЮзДДѓаЁЭъШЋЯрЭЌЃЉЃЌЦфжаАзЧђ3ИіЁЂКьЧђ2ИіЁЂКкЧђ1ИіЃЎ
ЃЈ1ЃЉЫцЛњДгДќжаШЁГівЛИіЧђЃЌЧѓШЁГіЕФЧђЪЧКкЧђЕФИХТЪЃЛ
ЃЈ2ЃЉШєШЁГіЕФЕквЛжЛЧђЪЧКьЧђЃЌВЛНЋЫќЗХЛиДќРяЃЌДгДќжагрЯТЕФЧђжадйЫцЛњЕиШЁГі1ИіЃЌетЪБШЁГіЕФЧђЪЧКкЧђЕФИХТЪЪЧЖрЩйЃП
ЃЈ3ЃЉШєШЁГівЛИіЧђЃЌНЋЫќЗХЛиДќжаЃЌДгДќжадйЫцЛњЕиШЁГівЛИіЧђЃЌСНДЮШЁГіЕФЧђЖМЪЧАзЧђЕФИХТЪЪЧЖрЩйЃПЃЈгУСаБэЗЈЛђЪїзДЭММЦЫуЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈm-1ЃЉx2-x-2=0ЃЌ
ЃЈ1ЃЉШєx=-1ЪЧЗНГЬЕФвЛИіИљЃЌЧѓmЕФжЕМАСэвЛИіИљЃЛ
ЃЈ2ЃЉЕБmЮЊКЮжЕЪБЗНГЬгаСНИіВЛЭЌЕФЪЕЪ§Иљ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЖдНЧЯпACгыBDЯрНЛгкЕуOЃЌдкDCЕФбгГЄЯпЩЯШЁвЛЕуEЃЌСЌНгOEНЛBCгкЕуFЃЎвбжЊAB=4ЃЌBC=6ЃЌCE=2ЃЌдђCFЕФГЄЕШгкЃЈ ЃЉ

A. 1 B. 1.5 C. 2 D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
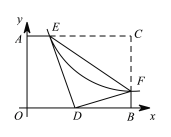
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§y=![]() (k>0)ЕФЭМЯёгыОиаЮAOBCЕФБпACЃЌBCЗжБ№НЛгкЕуEЁЂFЃЌЕуCЕФзјБъЮЊ(8ЃЌ6)ЃЌНЋЁїCEFбиEFЗелЃЌCЕуЧЁКУТфдкOBЩЯЕФЕуDДІЃЌдђkЕФжЕЮЊЃЈ ЃЉ
(k>0)ЕФЭМЯёгыОиаЮAOBCЕФБпACЃЌBCЗжБ№НЛгкЕуEЁЂFЃЌЕуCЕФзјБъЮЊ(8ЃЌ6)ЃЌНЋЁїCEFбиEFЗелЃЌCЕуЧЁКУТфдкOBЩЯЕФЕуDДІЃЌдђkЕФжЕЮЊЃЈ ЃЉ
A.![]() B.6C.12D.
B.6C.12D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
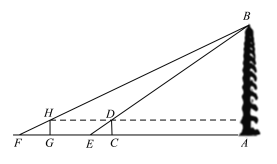
ЁОЬтФПЁПФГаЃЩчЛсЪЕМљаЁзщЮЊСЫВтСПДѓбуЫўЕФИпЖШЃЌдкЕиУцЩЯCДІДЙжБгкЕиУцЪњСЂСЫИпЖШЮЊ2УзЕФБъИЫCDЃЌДЫЪБЕиУцЩЯЕФЕуEЃЌБъИЫЕФЖЅЖЫЕуDЃЌДѓбуЫўЕФЫўМтЕуBе§КУдкЭЌвЛжБЯпЩЯЃЌВрЕУEC=4УзЃЌНЋБъИЫCDЯђКѓвЦЕНЕуGДІЃЌДЫЪБЕиУцЩЯЕФЕуFЃЌБъИЫЕФЖЅЖЫЕуHЃЌДѓбуЫўЕФЫўМтЕуBе§КУдкЭЌвЛжБЯпЩЯ(ЕуFЃЌЕуGЃЌЕуEЃЌЕуCгыЫўЕзДІЕФЕуAдкЭЌвЛжБЯпЩЯ)ЃЌетЪБВтЕУFG=6УзЃЌGC=53УзЃЌЧыФуИљОнвдЩЯЪ§ОнЃЌМЦЫуДѓбуЫўЕФИпЖШAB.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигк x ЕФКЏЪ§ y=ЃЈmЉ1ЃЉx2+2x+m ЭМЯѓгызјБъжсжЛга 2 ИіНЛЕуЃЌдђm=_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЧЪажаЁАДђГЕФбЁБвЛжБЪЧШЫУЧЙизЂЕФвЛИіЩчЛсШШЕуЮЪЬт.НќМИФъРДЃЌЁАЛЅСЊЭјЃЋЁБеНТдгыДЋЭГГізтГЕаавЕЩюЖШШкКЯЃЌЁАгХВНЁБЁЂЁАЕЮЕЮГіааЁБЕШДђГЕШэМўОЭЪЧЦфжаЕфаЭЕФгІгУЃЌУћЮЊЁАЪ§ОнАќТчЗжЮіЁБЃЈМђГЦDEAЃЉЕФвЛжжаЇТЪЦРМлЗНЗЈЃЌПЩвдКмКУЕигХЛЏГізтГЕзЪдДХфжУЃЌЮЊСЫНтГізтГЕзЪдДЕФЁАЙЉашЦЅХфЁБЃЌББОЉЁЂЩЯКЃЕШГЧЪаЖдУПЬь24ИіЪБЖЮЕФDEAжЕНјааЕїВщЃЌЕїВщЗЂЯжЃЌDEAжЕдНДѓЃЌЫЕУїЦЅХфЖШдНКУ.дкФГвЛЖЮЪБМфФкЃЌББОЉЕФDEAжЕyгыЪБПЬtЕФЙиЯЕНќЫЦТњзуКЏЪ§ЙиЯЕ![]() ЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌЧв
ЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌЧв![]() Ёй0ЃЉЃЌШчЭММЧТМСЫ3ИіЪБПЬЕФЪ§ОнЃЌИљОнКЏЪ§ФЃаЭКЭЫљИјЪ§ОнЃЌЕБЁАЙЉашЦЅХфЁБГЬЖШзюКУЪБЃЌзюНгНќЕФЪБПЬtЪЧЃЈ ЃЉ
Ёй0ЃЉЃЌШчЭММЧТМСЫ3ИіЪБПЬЕФЪ§ОнЃЌИљОнКЏЪ§ФЃаЭКЭЫљИјЪ§ОнЃЌЕБЁАЙЉашЦЅХфЁБГЬЖШзюКУЪБЃЌзюНгНќЕФЪБПЬtЪЧЃЈ ЃЉ

A. 4.8 B. 5 C. 5.2 D. 5.5
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com