
【题目】如图,在平行四边形ABCD中,点G是线段AB上一点,连接CG、DG,满足CG=CD.
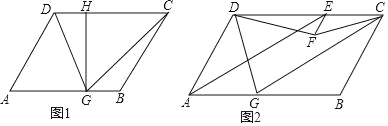
(1)如图1,过点G作GH⊥CD于点H,若AB=7,GH=2![]() ,求DG;
,求DG;
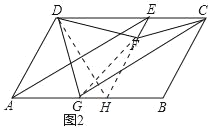
(2)如图2,若∠DAB=60°,∠DAB的角平分线交CD于点E,过点E作EF∥AD,满足EF+AG=AD,连接DF、CF,求证:∠DCF=∠GCF.
【答案】(1)DG=2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由平行四边形的性质和已知条件得出CG=CD=7,由勾股定理得出CH=![]() =5,得出DH=CD-CH=2,再由勾股定理即可得出结果;
=5,得出DH=CD-CH=2,再由勾股定理即可得出结果;
(2)延长EF交AB于H,连接DH、FG,先证明四边形ADEH是平行四边形,再由平行线的性质和角平分线证出∠AED=∠DAE,得出AD=ED,证出四边形ADEH是菱形,得出AD=ED=EH=AH,得出△ADH、△DEH是等边三角形,得出∠DHA=∠EDH=∠DEH=60°,DH=AD=DE,证出EF=GH,证明△DEF≌△DHG得出∠EDF=∠HDG,DF=DG,证出∠GDF=60°,得出△GDF是等边三角形,得出DF=GF,再证明△CDF≌△CGF,即可得出∠DCF=∠GCF.
(1)∵四边形ABCD是平行四边形,
∴CD=AB=7,
∵CG=CD=7,GH=2![]() ,BH⊥CD,
,BH⊥CD,
∴CH=![]() =
=![]() =5,
=5,
∴DH=CD﹣CH=2,
∴DG=![]() =2
=2![]() ;
;
(2)延长EF交AB于H,连接DH、FG,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AED=∠EAB,
∵EF∥AD,
∴四边形ADEH是平行四边形,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠AED=∠DAE,
∴AD=ED,
∴四边形ADEH是菱形,
∴AD=ED=EH=AH,
∵∠DAB=60°,
∴△ADH、△DEH是等边三角形,
∴∠DHA=∠EDH=∠DEH=60°,DH=AD=DE,
∵EF+AG=AD=AH=AG+GH,
∴EF=GH,
在△DEF和△DHG中,
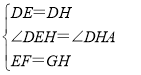 ,
,
∴△DEF≌△DHG(SAS),
∴∠EDF=∠HDG,DF=DG,
∴∠HDG+∠FDH=∠EDF+∠FDH=∠EDH=60°,即∠GDF=60°,
∴△GDF是等边三角形,
∴DF=GF,
在△CDF和△CGF中,
 ,
,
∴△CDF≌△CGF(SSS),
∴∠DCF=∠GCF.


科目:初中数学 来源: 题型:
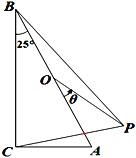
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学了统计知识后,小红就本班同学上学“喜欢的出行方式”进行了一次调查,图(1)和图(2)是她根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
(1)补全条形统计图,并计算出“骑车”部分所对应的圆心角的度数.
(2)若由3名“喜欢乘车”的学生,1名“喜欢骑车”的学生组队参加一项活动,现欲从中选出2人担任组长(不分正副),求出2人都是“喜欢乘车”的学生的概率,(要求列表或画树状图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点B,C在x轴上,反比例函数y=﹣![]() (x<0)的图象经过A,E两点,反比例函数y=
(x<0)的图象经过A,E两点,反比例函数y=![]() (x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(1)求点C的坐标及k的值;
(2)直接写出正方形EFGH的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A. ﹣![]() 或﹣12B. ﹣
或﹣12B. ﹣![]() 或2C. ﹣12或2D. ﹣
或2C. ﹣12或2D. ﹣![]() 或﹣12
或﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,CB⊥AB,D为圆上一点,且AD∥OC,连接CD,AC,BD,AC与BD交于点M.
(1)求证:CD为⊙O的切线;
(2)若CD=![]() AD,求
AD,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
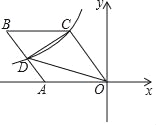
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=﹣
,反比例函数y=﹣![]() 的图象经过点C,与AB交与点D,则△COD的面积的值等于_____;
的图象经过点C,与AB交与点D,则△COD的面积的值等于_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com