
����Ŀ��ѧ��ͳ��֪ʶ��С��ͱ���ͬѧ��ѧ��ϲ���ij��з�ʽ��������һ�ε��飬ͼ��1����ͼ��2���������ݲɼ������ݻ��Ƶ�������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺
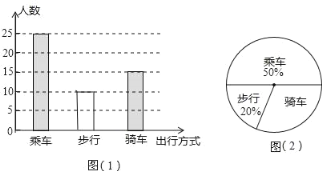
��1����ȫ����ͳ��ͼ������������ﳵ����������Ӧ��Բ�ĽǵĶ�����
��2������3����ϲ���˳�����ѧ����1����ϲ���ﳵ����ѧ����Ӳμ�һ������������ѡ��2�˵����鳤�����������������2�˶�����ϲ���˳�����ѧ���ĸ��ʣ���Ҫ���б�����״ͼ��

���𰸡���1����ȫ����ͳ��ͼ�����������ﳵ����������Ӧ��Բ�ĽǵĶ���Ϊ108�㣻��2��2�˶��ǡ�ϲ���˳�����ѧ���ĸ���Ϊ![]() ��
��
��������
��1������ͼ�п��Կ����˳�����25�ˣ�ռ��50%�����ɵù���ѧ��50�ˣ����������˳��ĺ��ﳵ���������Dz��е��������������ݲ�ȫֱ��ͼ���ɣ�Ҫ�����εĶ�����Ҫ������ﳵ��ռ�İٷֱȣ�Ȼ�������������2���г�����4����ѡ���˵����еȿ��ܽ������2�˶��ǡ�ϲ���˳�����ѧ���������3�֣�Ȼ����ݸ��ʹ�ʽ������ã�
��1���������������Ϊ25��50%��50�ˣ�
���е�����Ϊ50��25��15��10�ˣ�
��ͼ��ʾ����ͼ��
���ﳵ����������Ӧ��Բ�ĽǵĶ�����![]() ��360�㣽108�㣻
��360�㣽108�㣻
��2����3����ϲ���˳�����ѧ����ʾΪA��B��C��1����ϲ���ﳵ����ѧ����ʾΪD��
����AB��AC��AD��BC��BD��CD��6�ֵȿ��ܵ������
����2�˶��ǡ�ϲ���˳�����ѧ����3�ֽ����
����2�˶��ǡ�ϲ���˳�����ѧ���ĸ���Ϊ![]() ��
��


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ�궬�죬����������ѩ��Ϊȷ����·����ͨ�У������������˲�ѩ��������·����֪һ̨��ѩ���Ĺ���Ч���൱��һ���������˵�![]() ����һ̨��ѩ������
����һ̨��ѩ������![]() �����Ļ�ѩ��Ҫ��
�����Ļ�ѩ��Ҫ��![]() ����������������Щ��ѩ����
����������������Щ��ѩ����![]() Сʱ.
Сʱ.
(1)��һ̨��ѩ��ÿСʱ��ѩ����������?
(2)����һ����������Ҫ����![]() Сʱ���
Сʱ���![]() �����Ļ���������������������
�����Ļ���������������������![]() ̨��ѩ����
̨��ѩ����![]() ���������ˣ�������
���������ˣ�������![]() Сʱ���ֵ�����һЩ��ѩ������֧Ԯ���������������ֵ����˼�̨��ѩ�������������
Сʱ���ֵ�����һЩ��ѩ������֧Ԯ���������������ֵ����˼�̨��ѩ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�һ������һ�������㣬�������Ϊ1����һ�κ���
��ͼ���ڵ�һ������һ�������㣬�������Ϊ1����һ�κ���![]() ��ͼ������ǣ� ��
��ͼ������ǣ� ��
A. 
B. 
C. 
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��![]() ���������ν�ֱ��a��b�ڵ�A��B��C�͵�D��E��F.
���������ν�ֱ��a��b�ڵ�A��B��C�͵�D��E��F.
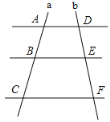
��1�����![]() ��
��![]() ��
��![]() ����DE�ij�.
����DE�ij�.
��2�����![]() ��
��![]() ��
��![]() ����BE�ij�.
����BE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ����������Ʒ�̵�һ���Թ������ɸ����������ÿ������ļ۸���ͬ��ÿ������ļ۸���ͬ��������1�������2��������270Ԫ������2�������3��������464Ԫ��
��1�������������ĵ��۸��Ƕ���Ԫ��
��2�����������������20�����ҹ�������ĸ������������������2������������ܷ��ò�����1910Ԫ���ʸ�ѧУ���ļ��ֲ�ͬ�Ĺ��������ַ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ADΪ��ABC�����ߣ���B��C����ֱ���AD����ֱ�ߵĴ��߶�BE��CF��E��FΪ���㣬����E��EG��AB��BC�ڵ�H������HF���ӳ���AB�ڵ�P��
��1����֤��DE=DF
��2����![]() ������
������![]() ��ֵ������֤���ı���HGAPΪƽ���ı��Ρ�
��ֵ������֤���ı���HGAPΪƽ���ı��Ρ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��УҪ���������ѡ����ѡ��һ���μ�ʡ�����˶��ᣬѡ������ÿ��ѡ���������10�Σ����Ǹ��Ե�ƽ���ɼ�![]() ���䷽��S2�����ʾ��
���䷽��S2�����ʾ��
�� | �� | �� | �� | |
������ | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
���Ҫѡ��һ���ɼ����ҷ����ȶ���ѡ�ֲ�������Ӧѡ���ѡ���ǣ� ��
A���� B���� C���� D����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���G���߶�AB��һ�㣬����CG��DG������CG��CD��
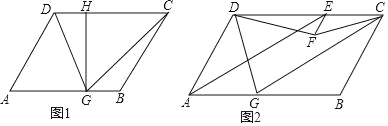
��1����ͼ1������G��GH��CD�ڵ�H����AB��7��GH��2![]() ����DG��
����DG��
��2����ͼ2������DAB��60�㣬��DAB�Ľ�ƽ���߽�CD�ڵ�E������E��EF��AD������EF+AG��AD������DF��CF����֤����DCF����GCF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��kx+b��k��0����ͼ���뷴��������y��![]() ��x��0��m��0����ͼ���ڵ�C����x�ᡢy��ֱ��ڵ�D��B����֪OB��3����C�ĺ�����Ϊ4��cos��0BD��
��x��0��m��0����ͼ���ڵ�C����x�ᡢy��ֱ��ڵ�D��B����֪OB��3����C�ĺ�����Ϊ4��cos��0BD��![]()
��1����һ�κ����������������ı���ʽ��
��2����һ�κ���ͼ������ƽ�ƣ�ʹ�侭��ԭ��O���뷴��������ͼ���ڵ��������ڵĽ���ΪA������AC�����ı���OACB�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com