
【题目】把一张矩形纸片ABC的按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F. 
(1)试在图中连接BE,求证:四边形BFB′E是菱形;
(2)若AB=8,BC=16,求线段BF长能取到的整数.
【答案】
(1)证明:连接BB′,如图1所示:
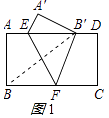
由折叠知点B、B′关于EF对称,
∴EF是线段BB′的垂直平分线,
∴BE=B′E,BF=B′F,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠B′EF=∠BFE,
由折叠得:∠B′FE=∠BFE,
∴∠B′EF=∠B′FE,
∴B′E=B′F,
∴BE=B′E=B′F=BF,
∴四边形BFB′E是菱形
(2)解:如图2所示:当点E与点A重合时,四边形ABFB′是正方形,此时BF最小,
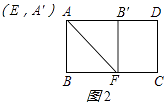
∵四边形ABFB′是正方形,
∴BF=AB=8,即BF最小为8;
如图2所示:当点B与点D重合时,BF最大,
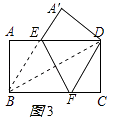
设BF=x,则CF=16﹣x,DF=BF=x,
在Rt△CDF中,由勾股定理得:CF2+CD2=DF2,
∴(16﹣x)2+82=x2,
解得:x=10,即BF=10,
∴8≤BF≤10,
∴线段BF长能取到的整数值为8,9,10.
【解析】(1)连接BB′,由折叠知点B、B′关于EF对称,得出EF是线段BB′的垂直平分线,证出BE=B′E,BF=B′F,由矩形的性质得出∠B′EF=∠BFE,由折叠得:∠B′FE=∠BFE,得出∠B′EF=∠B′FE,证出B′E=B′F,BE=B′E=B′F=BF,即可得出结论;(2)当点E与点A重合时,四边形ABFB′是正方形,此时BF最小,由正方形的性质得出BF=AB=8,得出BF最小为8; 当点B与点D重合时,BF最大,设BF=x,则CF=16﹣x,DF=BF=x,在Rt△CDF中,由勾股定理得出方程,解方程求出BF=10,得出8≤BF≤10,即可得出结果.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点. 
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
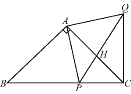
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形?若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.
(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.
《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”
设每头牛值金x两,每只羊值金y两,可列方程组为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com