
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
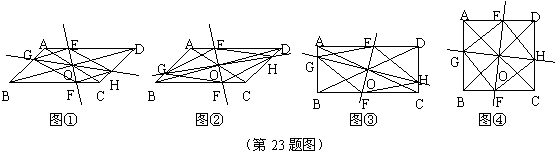
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
 |
解:(1)四边形EGFH是平行四边形.
 证明:∵ ABCD的对角线AC、BD交于点O.
证明:∵ ABCD的对角线AC、BD交于点O.
 ∴点O是 ABCD的对称中心.
∴点O是 ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形.
(2)菱形.
(3)菱形.
(4)四边形EGFH是正方形.


 ∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.∵EF⊥GH ,∴∠GOF=90°.
∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.∵EF⊥GH ,∴∠GOF=90°.
∴∠BOG=∠COF.∴△BOG≌△COF.∴OG=OF,∴GH=EF.
由(1)知四边形EGFH是平行四边形,又∵EF⊥GH,EF=GH.
∴四边形EGFH是正方形.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
如 图,已知锐角△ABC.
(1) 过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2) 在(1)条件下,若BC=5,AD=4,tan∠BAD=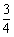 ,求DC的长.
,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果分别绘制了如下两个统计图。请根据图中提供的信息解答下列问题:
(1)图1中,“吸烟”类人数所占扇形的圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图
(4)若该市共有市民760万人,
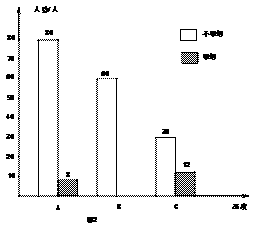 求该市大约有多少人吸烟?
求该市大约有多少人吸烟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com