
如 图,已知锐角△ABC.
(1) 过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2) 在(1)条件下,若BC=5,AD=4,tan∠BAD=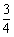 ,求DC的长.
,求DC的长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
在一个三角形中,各边和它所对角的正弦的比相等.即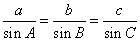 .利用上述结论可以求解如下题目.如:
.利用上述结论可以求解如下题目.如:
在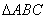 中,若
中,若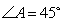 ,
,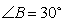 ,
,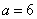 ,求
,求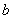 .
.
解:在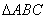 中,
中,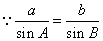
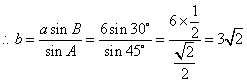
问题解决:
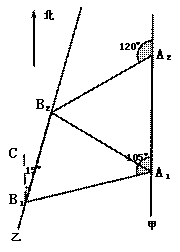
如图,甲船以每小时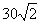 海里的速度向正北方航行,当甲船位于
海里的速度向正北方航行,当甲船位于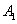 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西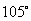 方向的
方向的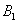 处,且乙船从
处,且乙船从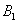 处按北偏东
处按北偏东 方向匀速直线航行,当甲船航行
方向匀速直线航行,当甲船航行 分钟到达
分钟到达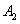 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西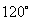 方向的
方向的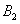 处,此时两船相距
处,此时两船相距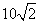 海里.
海里.
(1) 判断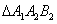 的形状,并给出证明.
的形状,并给出证明.
(2) 乙船每小时航行多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
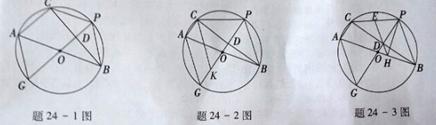
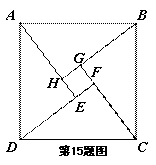
⊙O是△ABC的外接圆,AB是直径,过 的中点P作⊙O的直径PG交弦BC于点D,连接AG, CP,PB.
的中点P作⊙O的直径PG交弦BC于点D,连接AG, CP,PB.
(1) 如题24﹣1图;若D是线段OP的中点,求∠BAC的度数;
(2) 如题24﹣2图,在DG上取一点k,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;
(3) 如题24﹣3图;取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
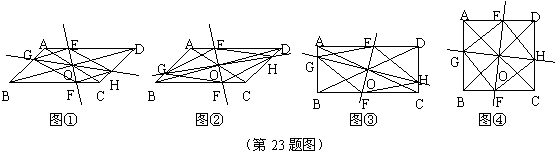
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
皮克定理”是来 计算原点在整点的多边形面积的公式,公式表达式为
计算原点在整点的多边形面积的公式,公式表达式为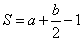 ,孔明只记得公式中的S表示多边形的面积,
,孔明只记得公式中的S表示多边形的面积,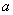 和
和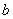 中有一个表示多边形那
中有一个表示多边形那 边上(含原点)的整点个数,另一个表示多边形内部的整点的个数,但不记得究竟是
边上(含原点)的整点个数,另一个表示多边形内部的整点的个数,但不记得究竟是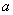 还是
还是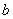 表示多边形内部的整点的个数,请你选
表示多边形内部的整点的个数,请你选 择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部整点个数的字母是 ;并运用这个公式求得如图2中多边形的面积是
择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部整点个数的字母是 ;并运用这个公式求得如图2中多边形的面积是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com