
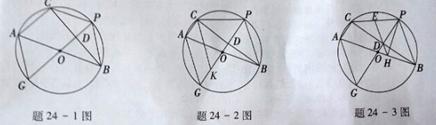
⊙O是△ABC的外接圆,AB是直径,过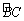 的中点P作⊙O的直径PG交弦BC于点D,连接AG, CP,PB.
的中点P作⊙O的直径PG交弦BC于点D,连接AG, CP,PB.
(1) 如题24﹣1图;若D是线段OP的中点,求∠BAC的度数;
(2) 如题24﹣2图,在DG上取一点k,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;
(3) 如题24﹣3图;取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.
【解析】(1) ∵AB为⊙O直径,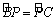 ,
,
∴PG⊥BC,即∠ODB=90°,
∵D为OP的中点,
∴OD= ,
,
∴cos∠BOD=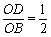 ,
,
∴∠BOD=60°,
∵AB为⊙O直径,
∴∠ACB=90°,
∴∠ACB=∠ODB,
∴AC∥PG,
∴∠BAC=∠BOD=60°;
(2) 由(1)知,CD=BD,
∵∠BDP=∠CDK,DK=DP,
∴△PDB≌△CDK,
∴CK=BP,∠OPB=∠CKD,
∵∠AOG=∠BOP,
∴AG=BP,
∴AG=CK
∵OP=OB,
∴∠OPB=∠OBP,
又∠G=∠OBP,
∴AG∥CK,
∴四边形AGCK是平行四边形;
(3) ∵CE=PE,CD=BD,
∴DE∥PB,即DH∥PB
∵∠G=∠OPB,
∴PB∥AG,
∴DH∥AG,
∴∠OAG=∠OHD,
∵OA=OG,
∴∠OAG=∠G,
∴∠ODH=∠OHD,
∴OD=OH,
又∠ODB=∠HOP,OB=OP,
∴△OBD≌△HOP,
∴∠OHP=∠ODB=90°,
∴PH⊥AB.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
2010年4月20日晚,“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行,热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为
A.3.1×106元 B.3.11×104元 C.3.1×104元 D.3.10×105元
查看答案和解析>>
科目:初中数学 来源: 题型:
某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出2张纸币.
(1) 求取出纸币的总额是30元的概率;
(2) 求取出纸币的总额可购买一件51元的商品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如 图,已知锐角△ABC.
(1) 过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2) 在(1)条件下,若BC=5,AD=4,tan∠BAD=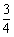 ,求DC的长.
,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
2010年4月20日晚,“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行,热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为
A.3.1×106元 B.3.11×104元 C.3.1×104元 D.3.10×105元
查看答案和解析>>
科目:初中数学 来源: 题型:
P表示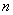 边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与
边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与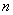 的关系式是:
的关系式是:
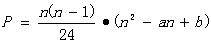
 (其中,
(其中,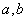 是常数,
是常数,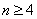 )
)
(1)填空:通过画图可得:
四边形时,P= (填数字),五边形时,,P= (填数字)
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求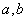 的值
的值
(注:本题的多边形均指凸多边形)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com